题目内容
15．已知-2≤a≤2，化简$\sqrt{（5-2a）}$-$\sqrt{（a+2）^{2}}$．分析 根据a的取值范围得出5-2a＞0，a+2＞0，进而化简求出即可．
解答 解：∵-2≤a≤2，
∴$\sqrt{（5-2a）}$-$\sqrt{（a+2）^{2}}$
=5-2a-（a+2）
=3-3a．
点评 此题主要考查了二次根式的性质与化简，正确得出5-2a，a+2的符号是解题关键．
练习册系列答案
相关题目
已知等腰Rt△ABC与等腰Rt△DBE，F为AE中点，G为CD中点，连结GF．判断FG与DC的位置关系和数量关系．
6．一个直角三角形两直角边的比为3：2，斜边上的高分得的两个直角三角形的面积分别为S1和S2（S1＜S2），则S1：S2=（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{4}{9}$ | D． | $\frac{1}{2}$ |
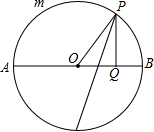如图，有一定圆O，直径为AB，今有一动点P在半圆AmB上移动，过点P作AB的垂线PQ，试证：∠OPQ的平分线恒通过一定点．
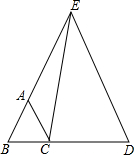已知BD=AE，AB=BC=CA，求证：EC=ED．
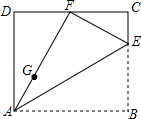如图，将矩形纸片ABCD沿直线AE折叠，点B恰好落在线段CD的中点F上，点G是线段AF上一动点（不与A，F重合），点G过GH⊥AB，垂足为H，将矩形沿直线GH翻折，点A恰好落在线段BH上点A′处．若AB长为8，则当△A′GE为直角三角形时，AH的长为$\frac{24-8\sqrt{3}}{3}$．