题目内容
14．
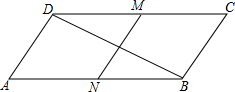已知：平行四边形ABCD，AB=2AD，∠A=60°，M，N分别是DC，AB中点．求证：MN⊥DB．
分析 利用直角三角形的判定方法结合平行四边形的性质和判定得出四边形ANMD是平行四边形，进而求出即可．
解答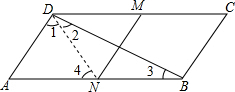 
解：连接DN，
∵AB=2AD，M，N分别是DC，AB中点，
∴AD=AN=BN，
又∵∠A=60°，
∴△ADN是等边三角形，
∴DN=AN=BN，
∴∠ADB=90°，
∵M，N分别是DC，AB中点，
∴AN=BN=DM=CM，
∵AB∥DC，
∴四边形ANMD是平行四边形，
∴AD∥MN，
∴MN⊥DB．
点评 本题考查了平行四边形的性质和判定，解答此题的关键是得出四边形ANMD是平行四边形．
练习册系列答案
特高级教师点拨系列答案
相关题目
4．下列说法中：①三角形中至少有2个角是锐角；②各边都相等的多边形是正多边形；③钝角三角形的三条高交于一点；④两个等边三角形全等；⑤三角形两个内角的平分线的交点到三角形三边的距离相等，正确的个数是（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
已知等腰Rt△ABC与等腰Rt△DBE，F为AE中点，G为CD中点，连结GF．判断FG与DC的位置关系和数量关系．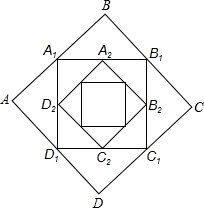
如图，正方形ABCD的边长为2，顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1，顺次连接正方形A1B1C1D1 四边的中点得到第二个正方形A2B2C2D2…以此类推，则第n个正方形AnBnCnDn的面积是（$\frac{1}{2}$）n-2．
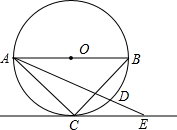已知AB为⊙O的直径，$\widehat{BD}$=2$\widehat{CD}$，CE∥AB切⊙O于C点，交AD延长线于E点，若⊙O半径为2cm，求AE的长．
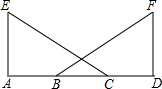如图，已知点A，B，C，D在同一条直线上，EA⊥AB，FD⊥AD，AB=CD，若用“HL”证明Rt△AEC≌△Rt△DFB，需添加什么条件？并写出你的证明过程．
6．一个直角三角形两直角边的比为3：2，斜边上的高分得的两个直角三角形的面积分别为S1和S2（S1＜S2），则S1：S2=（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{4}{9}$ | D． | $\frac{1}{2}$ |
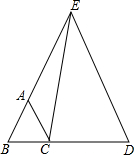已知BD=AE，AB=BC=CA，求证：EC=ED．