题目内容
12.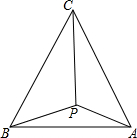 如图所示,P是正三角形ABC内一点,PA=2,PB=2$\sqrt{3}$,PC=4,求BC的长.
如图所示,P是正三角形ABC内一点,PA=2,PB=2$\sqrt{3}$,PC=4,求BC的长.
分析 先根据等边三角形的性质得CB=CA,∠ACB=90°,则利用旋转的定义,可把△CPA绕点C逆时针旋转60°得到△CDB,如图,作CH⊥BD于H,再根据旋转的性质得CD=CP═4,∠PCD=60°,BD=AP=2,于是可判断△CPD为等边三角形,得到∠PDC=60°,PD=CP=4,在△PDB中,利用勾股定理的逆定理得到∠PDB=90°,根据直角三角函数求得∠PDB=60°,然后根据平角定义可计算出∠CDH=60°,在Rt△CDH中,利用含30度的直角三角形三边的关系得DH=$\frac{1}{2}$CD=2,DH=$\frac{\sqrt{3}}{2}$CD=2$\sqrt{3}$,则BH=BD+DH=4,接着在Rt△BCH中,利用勾股定理计算出BC2=28,即可求得BC的长.
解答 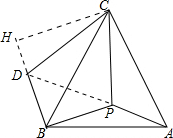 解:∵△ABC为等边三角形,
解:∵△ABC为等边三角形,
∴CB=CA,∠ACB=60°,
∴把△CPA绕点C逆时针旋转60°可得到△CDB,如图,作CH⊥BD于H,
∴CD=CP=4,∠PCD=60°,BD=AP=2,
∴△CPD为等边三角形,
∴∠PDC=60°,PD=CP=4,
在△PDB中,PB=2$\sqrt{3}$,BD=2,PD=4,
∵22+(2$\sqrt{3}$)2=42,
∴BD2+PB2=PD2,
∴△PDB为直角三角形,
∴∠PBD=90°,
∵cos∠PDB=$\frac{BD}{PD}$=$\frac{1}{2}$,
∴∠PDB=60°,
∴∠CDH=180°-60°-60°=60°,
在Rt△CDH中,DH=$\frac{1}{2}$CD=2,CH=$\frac{\sqrt{3}}{2}$CD=2$\sqrt{3}$,
∴BH=BD+DH=2+2=4,
在Rt△BCH中,BC2=BH2+CH2=42+(2$\sqrt{3}$)2=28,
∴BC=2$\sqrt{7}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质和勾股定理的逆定理.

| A. | a≥-1 | B. | a≥0 | C. | a≥1 | D. | a≤-1 |
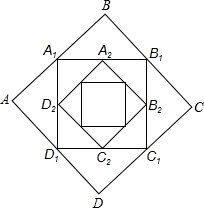 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,顺次连接正方形A1B1C1D1 四边的中点得到第二个正方形A2B2C2D2…以此类推,则第n个正方形AnBnCnDn的面积是($\frac{1}{2}$)n-2.
如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,顺次连接正方形A1B1C1D1 四边的中点得到第二个正方形A2B2C2D2…以此类推,则第n个正方形AnBnCnDn的面积是($\frac{1}{2}$)n-2.
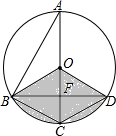 如图,已知在⊙O中,AB=2$\sqrt{3}$,AC是⊙O的直径,AC⊥BD于F,∠ABD=60°.
如图,已知在⊙O中,AB=2$\sqrt{3}$,AC是⊙O的直径,AC⊥BD于F,∠ABD=60°.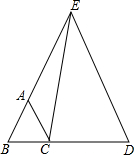 已知BD=AE,AB=BC=CA,求证:EC=ED.
已知BD=AE,AB=BC=CA,求证:EC=ED.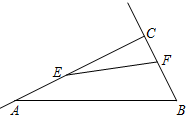 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.