题目内容
8.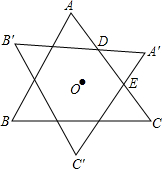 如图,将等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,交AC于点D,E,若以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.
如图,将等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,交AC于点D,E,若以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.
分析 分类讨论:当A′B′⊥AC于D,如图1,连结OA、OA′,根据等边三角形的性质和旋转的性质得OA=OA′,∠OAD=30°,∠OA′D=30°,则∠OAA′=∠OA′A,所以∠DAA′=∠DA′A,则DA=DA′,同理可得CE=A′E,在Rt△A′DE中,根据勾股定理可得A′D2+A′E2=DE2,即由AD2+CE2=DE2,再由DA=DA′得到∠DAA′=∠DA′A=45°,则根据三角形内角和可计算出∠AOA′=30°;当A′C′⊥AC于E,如图2,同理可得∠COA′=30°,根据等边三角形的性质得∠AOC=120°,则∠AOA′=90°,所以旋转角α=30°或90°.
解答 解:当A′B′⊥AC于D,如图1,连结OA、OA′,
∵等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,
∴OA=OA′,∠OAD=30°,∠OA′D=30°,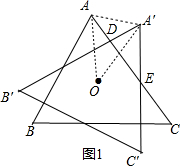
∴∠OAA′=∠OA′A,
∴∠DAA′=∠DA′A,
∴DA=DA′,
同理可得CE=A′E,
在Rt△A′DE中,A′D2+A′E2=DE2,
∴AD2+CE2=DE2,
∵DA=DA′,
∴∠DAA′=∠DA′A=45°,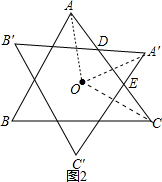
∴∠OAA′=∠OA′A=75°,
∴∠AOA′=30°,即旋转角α=30°;
当A′C′⊥AC于E,如图2,同理可得∠COA′=30°,
而∠AOC=120°,
∴∠AOA′=120°-30°=90°,即旋转角α=90°,
∴以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.
故答案为30°或90°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.

练习册系列答案
相关题目
6.一个直角三角形两直角边的比为3:2,斜边上的高分得的两个直角三角形的面积分别为S1和S2(S1<S2),则S1:S2=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
18.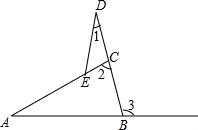 如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
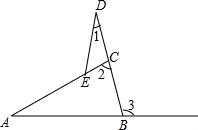 如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )
如图,在△ABC中,∠3是它的一个外角,E为边AC上一点,D在BC的延长上,则∠1、∠2、∠3之间的关系是( )| A. | ∠3>∠2>∠1 | B. | ∠2>∠3>∠1 | C. | ∠3=∠1+∠2 | D. | ∠1+∠2+∠3=180° |
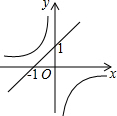
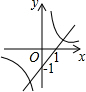
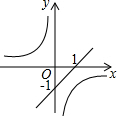
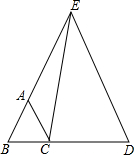 已知BD=AE,AB=BC=CA,求证:EC=ED.
已知BD=AE,AB=BC=CA,求证:EC=ED.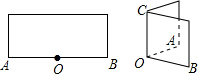 将一张长方形对折,使OA与OB重合,这时∠AOC是什么角?为什么?
将一张长方形对折,使OA与OB重合,这时∠AOC是什么角?为什么?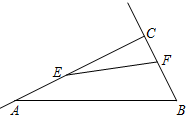 如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.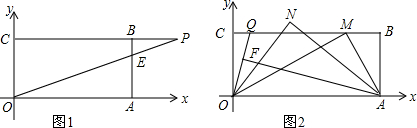
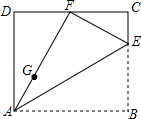 如图,将矩形纸片ABCD沿直线AE折叠,点B恰好落在线段CD的中点F上,点G是线段AF上一动点(不与A,F重合),点G过GH⊥AB,垂足为H,将矩形沿直线GH翻折,点A恰好落在线段BH上点A′处.若AB长为8,则当△A′GE为直角三角形时,AH的长为$\frac{24-8\sqrt{3}}{3}$.
如图,将矩形纸片ABCD沿直线AE折叠,点B恰好落在线段CD的中点F上,点G是线段AF上一动点(不与A,F重合),点G过GH⊥AB,垂足为H,将矩形沿直线GH翻折,点A恰好落在线段BH上点A′处.若AB长为8,则当△A′GE为直角三角形时,AH的长为$\frac{24-8\sqrt{3}}{3}$.