题目内容
19．某人要测河对岸的树高，在河边A处测得树顶仰角是60°，然后沿与河垂直的方向后退10米到B处，再测仰角是30°，求河对岸的树高．（精确到0.1米）分析 首先利用三角形的外角的性质求得∠ACB的度数，得到AC的长度，然后在直角△ADC中，利用三角函数即可求解．
解答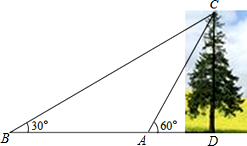 
解：如图∵∠CAD=60°，∠CAD=∠B+∠ACB，
∴∠ACB=∠CAD-∠B=60°-30°=30°，
∵∠B=30°，
∴∠B=∠ACB，
∵AB=10，
∴AC=AB=10，
在R△ACD中，CD=AC•sin∠CAD=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$≈8.7米．
点评 此题考查了解直角三角形的应用，用到的知识点是三角形的外角、特殊角的三角函数值、等腰三角形的性质，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
相关题目
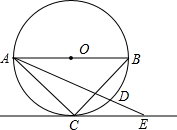已知AB为⊙O的直径，$\widehat{BD}$=2$\widehat{CD}$，CE∥AB切⊙O于C点，交AD延长线于E点，若⊙O半径为2cm，求AE的长．
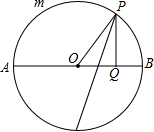如图，有一定圆O，直径为AB，今有一动点P在半圆AmB上移动，过点P作AB的垂线PQ，试证：∠OPQ的平分线恒通过一定点．
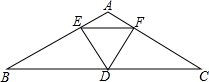如图，在△ABC中，∠A=120°，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，点E，F为垂足，求证：△DEF是等边三角形．
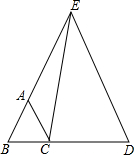已知BD=AE，AB=BC=CA，求证：EC=ED．
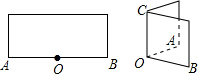将一张长方形对折，使OA与OB重合，这时∠AOC是什么角？为什么？