题目内容
11.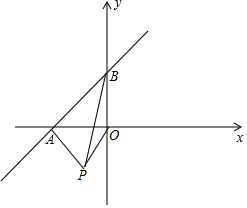 如图,一次函数y=x+2的函数图象与x轴,y轴分别交于点A,B.
如图,一次函数y=x+2的函数图象与x轴,y轴分别交于点A,B.(1)若点P(-1,m)为第三象限内一个动点,请问△OPB的面积会变化吗?若不变,请求出面积;若变化,请说明理由?
(2)在(1)的条件下,试用含m的代数式表示四边形APOB的面积;若△APB的面积是4,求m的值.
分析 (1)求出A、B点的坐标,利用三角形的面积公式即可得出结论;
(2)根据S四边形APOB=S△AOP+S△AOB即可得出四边形APOB的面积,再由△APB的面积是4可得出m的值.
解答 解:(1)不变.
∵一次函数y=x+2的函数图象与x轴,y轴分别交于点A,B,
∴A(-2,0),B(0,2),
∴OB=2.
∵P(-1,m),
∴S△OPB=$\frac{1}{2}$OB×1=$\frac{1}{2}$×2×1=1;
(2)∵A(-2,0),P(-1,m),
∴S四边形APOB=S△AOP+S△AOB=$\frac{1}{2}$OA•(-m)+$\frac{1}{2}$OA×2
=-$\frac{1}{2}$×2m+$\frac{1}{2}$×2×2
=2-m.
∵S四边形APOB=S△APB+S△OPB=4+1=5,
∴2-m=5,解得m=-3.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.关于x的不等式组$\left\{\begin{array}{l}3x-1>4({x-1})\\ x<a\end{array}\right.$的解集为x<3,那么a的取值范围为( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
2.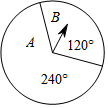 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )
 如图,让转盘自由转动一次,则指针落在A区域的概率是( )
如图,让转盘自由转动一次,则指针落在A区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
6. 如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )
如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )
 如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )
如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )| A. | 15秒 | B. | 20秒 | C. | 15秒或25秒 | D. | 15秒或20秒 |
3.已知∠α是锐角,∠β是钝角,且∠α+∠β=180°,那么下列结论正确的是( )
| A. | ∠α的补角和∠β的补角相等 | B. | ∠α的余角和∠β的补角相等 | ||
| C. | ∠α的余角和∠β的补角互余 | D. | ∠α的余角和∠β的补角互补 |
20.为执行“两免一补”政策,某地区2006年投入教育经费2500万元,预计2008年投入3600万元,设这两年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )
| A. | 2500(1+x)+2500(1+x)2=3600 | B. | 2500(1+x%)2=3600 | ||
| C. | 2500x2=3600 | D. | 2500(1+x)2=3600 |

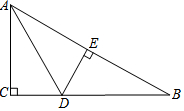 如图,在 Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB于点E,若CD=2,则DE的长为( )
如图,在 Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB于点E,若CD=2,则DE的长为( ) 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.