题目内容
6．
如图，数轴上点A，B表示的数分别为-40，50．现有一动点P以2个单位每秒的速度从点A向B运动，另一动点Q以3个单位每秒的速度从点B向A运动．当AQ=3PQ时，运动的时间为（ ）| A． | 15秒 | B． | 20秒 | C． | 15秒或25秒 | D． | 15秒或20秒 |
分析 根据点A，B表示的数，分两种情况：P、Q相遇前，P、Q相遇后，结合AQ=3PQ即可得出关于t的一元一次方程，解之即可得出结论．
解答 解：设运动的时间为t 秒，
P、Q相遇前，
依题意有
50-（-40）-3t=3[50-（-40）-2t-3t]，
解得t=15；
P、Q相遇后，
依题意有
50-（-40）-3t=3t=3[2t+3t-50+（-40）]，
解得t=20．
故运动的时间为15秒或20秒．
故选：D．
点评 本题考查了一元一次方程的应用、数轴以及两点间的距离，根据数量关系列出关于时间t的一元一次方程是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．不等式2x-1＜3的解集在数轴上表示为（ ）
| A． |  | B． |  | C． |  | D． |  |
1．-$\frac{3}{4}$的相反数是（ ）
| A． | $-\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{3}$ | D． | $-|{\frac{3}{4}}|$ |
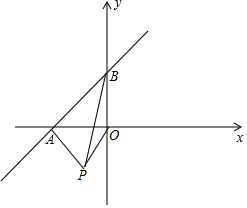如图，一次函数y=x+2的函数图象与x轴，y轴分别交于点A，B．
在如图所示的正方形网格中，每个小正方形的边长皆为1．请在网格上画出长度分别为$\sqrt{2}$，$\sqrt{5}$，$\sqrt{17}$的线段．