题目内容
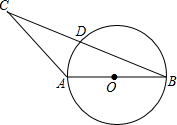 如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.
如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.考点:点与圆的位置关系
专题:
分析:要求D与⊙O的位置关系,需先求OD的长,再与其半径相比较;若大于半径则在圆外,等于半径在圆上,小于半径则在圆内.
解答: 解:点D在⊙O上.
解:点D在⊙O上.
理由如下:
连接OD,
∵BD=DC,BO=OA,
∴OD是△BAC的中位线,
∴OD=
AC,
∵AB=AC=4,
∴OD=
AB=2,
∴点D在⊙O上.
 解:点D在⊙O上.
解:点D在⊙O上.理由如下:
连接OD,
∵BD=DC,BO=OA,
∴OD是△BAC的中位线,
∴OD=
| 1 |
| 2 |
∵AB=AC=4,
∴OD=
| 1 |
| 2 |
∴点D在⊙O上.
点评:此题主要考查了点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP=d,则有:①点P在圆外?d>r;②点P在圆上?d=r;③点P在圆内?d<r.同时考查了三角形中位线定理.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动.
在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从点C出发沿CB边向点B以2cm/s的速度移动.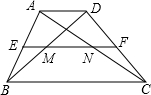 如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.
如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长. 如图,在△ABC中,∠ACB=∠ABC,∠A=50°,点P是△ABC内一点,且∠1=∠2,试求∠P的度数.
如图,在△ABC中,∠ACB=∠ABC,∠A=50°,点P是△ABC内一点,且∠1=∠2,试求∠P的度数.