题目内容
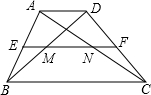 如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.
如图,在梯形ABCD中,AD∥BC,中位线EF=2.6cm,EF分别交AC、BD于点N、M,且MN=0.8cm,求AD、BC的长.考点:梯形中位线定理
专题:
分析:先由梯形中位线定理,得出EF∥AD∥BC,EF=
(AD+BC),又EF分别交AC、BD于点N、M,得到M、N分别为BD、AC中点,根据三角形中位线定理得出EM=
AD,FN=
AD,设AD=x,则EM=FN=
x,根据EM+MN+FN=EF列出方程
x+0.8+
x=2.6,解方程求出AD=1.8cm,然后根据EF=
(AD+BC),即可求出BC=3.4cm.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵EF为梯形ABCD的中位线,
∴EF∥AD∥BC,EF=
(AD+BC),
∵EF分别交AC、BD于点N、M,
∴M、N分别为BD、AC中点,
∴EM、FN分别是△ABD、△ACD的中位线,
∴EM=
AD,FN=
AD,
设AD=x,则EM=FN=
x,
∵EM+MN+FN=EF,
∴
x+0.8+
x=2.6,
∴x=1.8,即AD=1.8cm.
∵EF=
(AD+BC),
∴2.6=
(1.8+BC),
∴BC=3.4cm.
∴EF∥AD∥BC,EF=
| 1 |
| 2 |
∵EF分别交AC、BD于点N、M,
∴M、N分别为BD、AC中点,
∴EM、FN分别是△ABD、△ACD的中位线,
∴EM=
| 1 |
| 2 |
| 1 |
| 2 |
设AD=x,则EM=FN=
| 1 |
| 2 |
∵EM+MN+FN=EF,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴x=1.8,即AD=1.8cm.
∵EF=
| 1 |
| 2 |
∴2.6=
| 1 |
| 2 |
∴BC=3.4cm.
点评:本题考查了梯形中位线定理:梯形的中位线平行于两底,并且等于两底和的一半.同时考查了三角形中位线定理.

练习册系列答案
相关题目
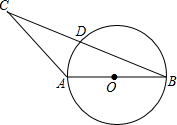
 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的同侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的同侧,AB=24cm,CD=10cm,求AB和CD的距离.
 如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.
如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系. 如图,在△ABC中,∠A=150°,AB=AC=6cm,求△ABC的面积.
如图,在△ABC中,∠A=150°,AB=AC=6cm,求△ABC的面积. 如图,△ABC为等边三角形,D是AC的中点,E是BC延长线上一点,且CE=
如图,△ABC为等边三角形,D是AC的中点,E是BC延长线上一点,且CE=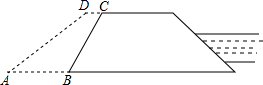 由于发生大洪水,需要加固一段大堤,计划使大堤加宽1m,使坡度由原来的1:2变成1:3.已知原来BC=12m,堤长100m,那么需要砂石和土多少立方米?
由于发生大洪水,需要加固一段大堤,计划使大堤加宽1m,使坡度由原来的1:2变成1:3.已知原来BC=12m,堤长100m,那么需要砂石和土多少立方米?