题目内容
 如图,在△ABC中,∠ACB=∠ABC,∠A=50°,点P是△ABC内一点,且∠1=∠2,试求∠P的度数.
如图,在△ABC中,∠ACB=∠ABC,∠A=50°,点P是△ABC内一点,且∠1=∠2,试求∠P的度数.考点:三角形内角和定理
专题:
分析:首先根据命题中∠ACB=∠ABC,∠1=∠2的条件,得到∠ACP=∠ABP,进而求出∠1+∠PCB的值;再次运用三角形的内角和定理即可解决问题.
解答:解:∵∠ACB=∠ABC,∠1=∠2(设为x)
∴∠ACP=∠ABP(设为y);
∵∠A=50°,
∴∠ACB+∠ABC=2(x+y)=180°-50°=130°;
故x+y=65°;
故∠P=180°-(x+y)=115°,即∠P=115°.
∴∠ACP=∠ABP(设为y);
∵∠A=50°,
∴∠ACB+∠ABC=2(x+y)=180°-50°=130°;
故x+y=65°;
故∠P=180°-(x+y)=115°,即∠P=115°.
点评:考查了三角形的内角和定理及其应用问题;解题的关键是根据图形中角与角之间的关系,灵活运用三角形的内角和定理解题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
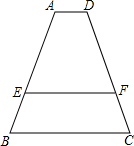 如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=
如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=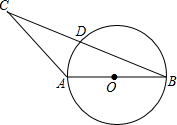 如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.
如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系. 如图,△ABC为等边三角形,D是AC的中点,E是BC延长线上一点,且CE=
如图,△ABC为等边三角形,D是AC的中点,E是BC延长线上一点,且CE= 如图,在△ABC中,AD是BC边上的中线,BE是AC边上的中线,BE交AD于F,那么
如图,在△ABC中,AD是BC边上的中线,BE是AC边上的中线,BE交AD于F,那么 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,DE⊥AB于点E,AD=4,求BE的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,DE⊥AB于点E,AD=4,求BE的长.