题目内容
现有100个整数a1,a2,a3,…,a99,a100,同时满足下列四个条件:
①-1≤ai≤2(i=1,2,3,…,99,100);
②a1+a2+a3+…+a99+a100=60;
③a12+a22+a32+…+a992+a1002=160;
④a13+a23+a33+…+a993+a1003=180.
求a14+a24+a34+…+a994+a1004的平方根.
①-1≤ai≤2(i=1,2,3,…,99,100);
②a1+a2+a3+…+a99+a100=60;
③a12+a22+a32+…+a992+a1002=160;
④a13+a23+a33+…+a993+a1003=180.
求a14+a24+a34+…+a994+a1004的平方根.
考点:有理数无理数的概念与运算
专题:整体思想
分析:不妨设这100个整数中有a个-1,b个0,c个1,d个2,则a14+a24+a34+…+a994+a1004=a+c+16d.根据题意可得到关于a、b、c、d的方程组,求出a、b、c、d的值,就可解决问题.
解答:解:设这100个整数中有a个-1,b个0,c个1,d个2,
则a14+a24+a34+…+a994+a1004=a+c+16d.
根据题意可得:
,
解得:
,
∴a+c+16d=30+50+16×20=400,
即a14+a24+a34+…+a994+a1004=400.
∴a14+a24+a34+…+a994+a1004的平方根为±20.
则a14+a24+a34+…+a994+a1004=a+c+16d.
根据题意可得:
|
解得:
|
∴a+c+16d=30+50+16×20=400,
即a14+a24+a34+…+a994+a1004=400.
∴a14+a24+a34+…+a994+a1004的平方根为±20.
点评:本题考查了解方程组、求平方根等知识,运用整体思想是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在菱形ABCD中,AB=5,∠ABC=120°,则对角线BD等于( )
如图,在菱形ABCD中,AB=5,∠ABC=120°,则对角线BD等于( )| A、20 | B、15 | C、10 | D、5 |
下列一元二次方程用配方法解比较简单的是( )
| A、x2-x-5=0 |
| B、(x-2)2=5 |
| C、x2+4x-6=0 |
| D、x2-3x=0 |
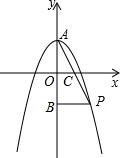 如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.
如图,抛物线y=ax2+2与y轴交于点A,抛物线上的一点P在第四象限,连接AP与x轴交于点C,若AC=PC,且S△AOC=1,记点A关于x轴的对称点为B.连结BP.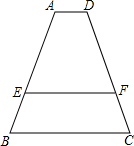 如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=
如图,已知AD∥EF∥BC,AD=2,BC=6,AE2=AB•EB,则EF=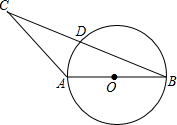 如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.
如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.