题目内容
18.(1)计算:(-1)5-${(\frac{1}{3})}^{-2}$÷(-3)-${({2\sqrt{3}})^2}$;(2)化简:($\frac{{b}^{2}}{{a}^{2}{-b}^{2}}$+1)•$\frac{{a}^{2}+2ab{+b}^{2}}{{a}^{2}}$.
分析 (1)根据负整数指数幂和有理数的除法和减法可以解答本题;
(2)根据分式的加法和乘法可以解答本题.
解答 解:(1)(-1)5-${(\frac{1}{3})}^{-2}$÷(-3)-${({2\sqrt{3}})^2}$
=-1-9÷(-3)-12
=-1+3-12
=-10;
(2)($\frac{{b}^{2}}{{a}^{2}{-b}^{2}}$+1)•$\frac{{a}^{2}+2ab{+b}^{2}}{{a}^{2}}$
=$\frac{a^2}{{{a^2}-{b^2}}}•\frac{{{a^2}+2ab+{b^2}}}{a^2}$
=$\frac{a^2}{{({a+b})({a-b})}}•\frac{{{{({a+b})}^2}}}{a^2}$
=$\frac{a+b}{a-b}$.
点评 本题考查分式的混合运算、实数的运算、负整数指数幂,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
16. 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
13.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上的中线的比为( )
| A. | 2:3 | B. | 4:16 | C. | 3:2 | D. | 16:4 |
 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是AC=BD.(写一种即可)
如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是AC=BD.(写一种即可)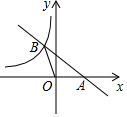 如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )
如图,直线y=-$\frac{1}{2}$x+b与x轴交于点A,与双曲线y=-$\frac{4}{x}$(x<0)交于点B,若S△AOB=2,则b的值是( )