题目内容
3.已知:如图,一次函数y1=x+5的图象与反比例函数y2=$\frac{k}{x}$的图象交于A、B两点,当x>1时,y1>y2;当0<x<1时,y1<y2.(1)直接写出反比例函数y2的解析式;
(2)过点D(t,0)(t>0)作x轴的垂线,分别交双曲线y2=$\frac{k}{x}$和直线y1=x+5于P、Q两点,若PQ=3PD时,求t的值;
(3)若直线l过点D(-2,-3),且与函数y=$\frac{k}{|x|}$的图象恰好有2个交点.
①在网格中画出y=$\frac{k}{|x|}$的图象;
②请直接写出直线l的解析式.
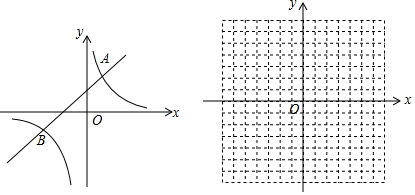
分析 (1)根据当x>1时,y1>y2;当0<x<1时,y1<y2,可得A点的横坐标是1,进而得出A(1,6),代入y2=$\frac{k}{x}$,可得k的值;
(2)设P(t,$\frac{6}{t}$),Q(t,t+5),根据PQ=3PD,可得方程t+5-$\frac{6}{t}$=3×$\frac{6}{t}$,进而得到t的值;
(3)①根据函数y=$\frac{k}{|x|}$画出其图象即可;②设直线l的解析式为y=mx+2m-3,令$\frac{6}{-x}$=mx+2m-3,则mx2+(2m-3)x+6=0,根据直线l与函数y=$\frac{6}{-x}$(x<0)相切,即可得到△=(2m-3)2-4m×6=0,得出m的值即可得到直线l的解析式.
解答 (1)∵当x>1时,y1>y2;当0<x<1时,y1<y2,
∴A点的横坐标是1,纵坐标为y=1+5=6,
∴A(1,6),
代入y2=$\frac{k}{x}$,可得k=xy=6,
∴y2=$\frac{6}{x}$;
(2)如图所示,当PQ=3PD时,直线PQ在点A的右侧,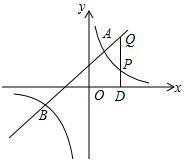
∵直线PQ分别交双曲线y2=$\frac{k}{x}$和直线y1=x+5于P、Q两点,
∴P(t,$\frac{6}{t}$),Q(t,t+5),
∵PQ=3PD,
∴t+5-$\frac{6}{t}$=3×$\frac{6}{t}$,
解得t1=3,t2=-8(舍去)
∴t的值为3;
(3)①y=$\frac{k}{|x|}$的图象如图所示:
②设过点D的直线l为y=mx+n,
把D(-2,-3)代入,可得-3=-2m+n,
∴n=2m-3,
∴直线l的解析式为y=mx+2m-3,
当x<0时,y=$\frac{6}{-x}$,
令$\frac{6}{-x}$=mx+2m-3,则mx2+(2m-3)x+6=0,
∵直线l与函数y=$\frac{6}{|x|}$的图象恰好有2个交点,
∴直线l与函数y=$\frac{6}{-x}$(x<0)相切,
令$\frac{6}{-x}$=mx+2m-3,则mx2+(2m-3)x+6=0,
∴△=(2m-3)2-4m×6=0,
解得m1=$\frac{9+6\sqrt{2}}{2}$,m2=$\frac{9-6\sqrt{2}}{2}$(舍去)
∴直线l的解析式为y=$\frac{9+6\sqrt{2}}{2}$x+6+6$\sqrt{2}$.
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点坐标同时满足反比例函数与一次函数的解析式.解决问题的关键是画出函数图象,根据函数图象的交点数量进行求解.

 完成下面的证明.
完成下面的证明.