题目内容
16. 如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )
如图,AE=AC,AB=AD,∠EAB=∠CAD,则图中全等三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
分析 根据全等三角形的判定定理可证出△EAD≌△CAB(SAS)、△EAM≌△CAN(ASA)、△ABN≌△ADM(SAS)和△BOM≌△DON(AAS),由此即可得出有4对全等的三角形,此题得解.
解答 解:∵∠EAB=∠CAD,
∴∠EAD=∠CAB.
在△EAD和△CAB中,$\left\{\begin{array}{l}{AE=AC}\\{∠EAD=∠CAB}\\{AD=AB}\end{array}\right.$,
∴△EAD≌△CAB(SAS),
∴∠E=∠C,∠D=∠B.
在△EAM和△CAN中,$\left\{\begin{array}{l}{∠E=∠C}\\{AE=AC}\\{∠EAM=∠CAN}\end{array}\right.$,
∴△EAM≌△CAN(ASA),
∴AM=AN.
∵AB=AD,
∴BM=DN.
在△ABN和△ADM中,$\left\{\begin{array}{l}{AN=AM}\\{∠BAN=∠DAM}\\{AB=AD}\end{array}\right.$,
∴△ABN≌△ADM(SAS).
在△BOM和△DON中,$\left\{\begin{array}{l}{∠BOM=∠DON}\\{∠B=∠D}\\{BM=DN}\end{array}\right.$,
∴△BOM≌△DON(AAS).
综上所述:全等的三角形有△EAD≌△CAB、△EAM≌△CAN、△ABN≌△ADM和△BOM≌△DON.
故选B.
点评 本题考查了全等三角形的判定,牢记全等三角形的5种判定方法是解题的关键.

练习册系列答案
相关题目
6.苏州市5月中旬每天平均空气质量指数(AQI)分别为:84,89,83,99,69,73,78,81,89,82,为了描述这十天空气质量的变化情况,最适合用的统计图是( )
| A. | 折线统计图 | B. | 频数分布直方图 | C. | 条形统计图 | D. | 扇形统计图 |
7.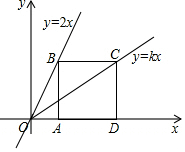 如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
 如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )
如图,边长为2的正方形ABCD的边AD在x轴的正半轴上,点B和点C分别在直线y=2x和直线y=kx上,则k的值是( )| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
4.下列命题中正确的为( )
| A. | 相等的圆心角所对的弦相等 | B. | 长度相等的弧是等弧 | ||
| C. | 等弧所对圆周角相等 | D. | 等弦所对圆周角相等 |
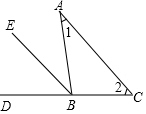 如图,已知在△ABC中,∠1=∠2.
如图,已知在△ABC中,∠1=∠2.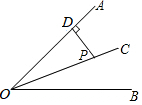 如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.