题目内容
6.已知x=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$,y=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,求下列各式的值(1)x2-y2
(2)$\frac{y}{x}$+$\frac{x}{y}$.
分析 (1)先把x,y分母有理化,再根据平方差公式计算即可;
(2)先通分,再计算即可.
解答 解:(1)∵x=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$,y=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$,
∴x=($\sqrt{2}$+1)2,y=($\sqrt{2}$-1)2,
∴x2-y2=($\sqrt{2}$+1)4•($\sqrt{2}$-1)4=[($\sqrt{2}$+1)($\sqrt{2}-1$)]4=1;
(2)$\frac{y}{x}$+$\frac{x}{y}$=$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{(3+2\sqrt{2})^{2}+(3-2\sqrt{2})^{2}}{1}$=34.
点评 本题考查了分母有理化,掌握有理化因式的找法是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
4.下列命题中正确的为( )
| A. | 相等的圆心角所对的弦相等 | B. | 长度相等的弧是等弧 | ||
| C. | 等弧所对圆周角相等 | D. | 等弦所对圆周角相等 |
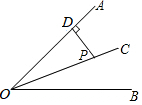 如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.
如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,垂足为D,若PD=$\sqrt{3}$,则点P到OB的距离是$\sqrt{3}$.