题目内容
3．
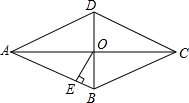如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=128°，则∠AOE的大小为（ ）| A． | 62° | B． | 52° | C． | 68° | D． | 64° |
分析 先根据菱形的邻角互补求出∠BAD的度数，再根据菱形的对角线平分一组对角求出∠BAO的度数，然后根据直角三角形两锐角互余列式计算即可得解．
解答 解：在菱形ABCD中，∠ADC=128°，
∴∠BAD=180°-128°=52°，
∴∠BAO=$\frac{1}{2}$∠BAD=$\frac{1}{2}$×52°=26°，
∵OE⊥AB，
∴∠AOE=90°-∠BAO=90°-26°=64°．
故选D．
点评 本题主要考查了菱形的邻角互补，每一条对角线平分一组对角的性质，直角三角形两锐角互余的性质，熟练掌握性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．如图是某一计算程序，例如：当输入x=150时，输出结果是301；当输入x=100时，输出结果是403；若输入x的值是正整数，输出结果是407，则满足条件的x的值最多有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
14．已知x＞2，则下列变形正确的是（ ）
| A． | -x＜2 | B． | 若y＞2，则x-y＞0 | C． | -$\frac{1}{2}$x+2＜1 | D． | 若y＞2，则$\frac{x}{y}＞1$ |
如图，A、B、C是数轴上的三个点，它们分别表示三个数是a、b、c，其中b=1．
小明在荡秋千时，发观秋千在静止时，秋千离地面3dm（EF=3dm），荡起的水平距离为13dm（BC=13dm）时，离地面8dm（BD=8dm），求秋千的绳索AF的长．