题目内容
15．（1）若A=x2+4xy+y2-4，B=4x+4xy-6y-25，则比较A、B的大小关系；（2）若（x+2）（x2+mx+4）的展开式中不含有x的二次项，求m的值．
分析 （1）把A与B代入A-B中，去括号合并得到最简结果，判断差的正负即可确定出A与B的大小；
（2）原式利用多项式乘以多项式法则计算，根据结果不含x的二次项，确定出m的值即可．
解答 解：（1）∵A=x2+4xy+y2-4，B=4x+4xy-6y-25，
∴A-B=（x2+4xy+y2-4）-（4x+4xy-6y-25）=x2+y2-4x+6y+21=（x-2）2+（y+3）2+8，
∵（x-2）2+（y+3）2+8≥8＞0，
∴A-B＞0，
∴A、B的大小关系为：A＞B；
（2）（x+2）（x2+mx+4）=x3+（m+2）x2+（2m+4）x+8，
由展开式中不含x2项，得到m+2=0，则m=-2．
点评 此题考查了因式分解的应用，非负数的性质，以及多项式乘多项式，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
6．
如图，△ABC中，AB=AC，点D在AC边上，若AD=BD=BC，则∠A的度数为（ ）
如图，△ABC中，AB=AC，点D在AC边上，若AD=BD=BC，则∠A的度数为（ ）| A． | 70° | B． | 45° | C． | 36° | D． | 30° |
3．
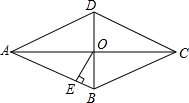如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=128°，则∠AOE的大小为（ ）
如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=128°，则∠AOE的大小为（ ）| A． | 62° | B． | 52° | C． | 68° | D． | 64° |
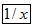，能求出输入的不为零的数的倒数（注：有时需先按
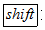或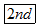
键，才能实现此功能，下面不再说明）．例如，输入2，按下键
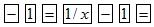，在显示屏上的结果是-0.75，则原来输入的某数是5．
20．对于实数a、b，规定a⊕b=a-2b，若4⊕（x-3）=2，则x的值为（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | $\frac{5}{2}$ | D． | 4 |
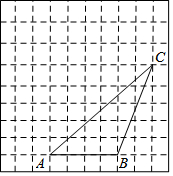如图，△ABC的顶点都在方格纸的格点上，将△ABC向左平移1格，再向上平移3格，其中每个格子的边长为1个单位长度．