题目内容
4. 如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=12cm,求△ODE周长.
如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=12cm,求△ODE周长.
分析 由BO为∠ABC的平分线,得到一对角相等,再由OD与AB平行,根据两直线平行内错角相等得到一对角相等,等量代换得到∠DBO=∠DOB,再由等角对等边得到OD=BD,同理OE=CE,然后利用三边之和表示出三角形ODE的周长,等量代换得到其周长等于BC的长,由BC的长即可求出三角形ODE的周长.
解答 解:∵BO平分∠ABC,
∴∠ABO=∠DBO,
又∵OD∥AB,
∴∠ABO=∠DOB,
∴∠DBO=∠DOB,
∴OD=BD,
同理OE=CE,
∵BC=12cm,
∴△ODE的周长c=OD+DE+OE=BD+DE+EC=BC=12cm.
点评 此题考查了等腰三角形的判定与性质,以及平行线的性质,利用了等量代换的思想,熟练掌握性质是解本题的关键.

练习册系列答案
相关题目
12.若ax2+bx+c<0(a≠0)无解,则a,b,c应满足( )
| A. | a>0,△≤0 | B. | a>0,△>0 | C. | a<0,△<0 | D. | a<0,△≤0 |
 如图,把一个圆柱形木块沿它的轴部剖开,得矩形ABCD.已知AD=8cm,AB=14cm.求这个圆柱形木块的表面积(π≈3.1,精确到1cm2)
如图,把一个圆柱形木块沿它的轴部剖开,得矩形ABCD.已知AD=8cm,AB=14cm.求这个圆柱形木块的表面积(π≈3.1,精确到1cm2)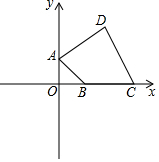 已知:如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(0,1)、B(1,0)、C(3,0)、D(2,2),求四边形ABCD的面积.
已知:如图,在平面直角坐标系中,四边形ABCD四个顶点的坐标分别为A(0,1)、B(1,0)、C(3,0)、D(2,2),求四边形ABCD的面积. 如图,正方形的边长为1dm,剪去四个角后成为一个正八边形.求这个正八边形的边长和面积.
如图,正方形的边长为1dm,剪去四个角后成为一个正八边形.求这个正八边形的边长和面积. 在Rt△ABC中,AC=3,BC=4,∠ACB=90°.若以点C为圆心,r为半径的圆与直线AB不相离,求r的取值范围.
在Rt△ABC中,AC=3,BC=4,∠ACB=90°.若以点C为圆心,r为半径的圆与直线AB不相离,求r的取值范围.