题目内容
12．若ax2+bx+c＜0（a≠0）无解，则a，b，c应满足（ ）| A． | a＞0，△≤0 | B． | a＞0，△＞0 | C． | a＜0，△＜0 | D． | a＜0，△≤0 |
分析 不等式的解集为空集即二次函数y=ax2+bx+c开口向上得到a大于0，且x轴的交点有一个或没有交点得到△≤0，即可得到满足的条件．
解答 解：设y=ax2+bx+c，要使ax2+bx+c＜0（a≠0）无解，
如图所示，即要二次函数开口向上且与x轴没有或只有一个交点即a＞0且b2-4ac≤0，
所以系数a，b．c应当满足的条件为a＞0且b2-4ac≤0．
故选：A．
点评 本题主要考查一元二次不等式的概念，解决问题的关键是利用二次函数与一元二次不等式的关系解决实际问题．
练习册系列答案
阅读快车系列答案
相关题目
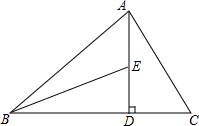如图，在△ABC中，∠ABC=45°，AD⊥BC于点D，点E在AD上，且BE=AC，观察并猜想线段DE与线段CD的大小关系，然后证明你的猜想．
20．下列二次根式中，最简二次根式的是（ ）
| A． | $\sqrt{\frac{1}{5}}$ | B． | $\sqrt{0.5}$ | C． | $\sqrt{5}$ | D． | $\sqrt{50}$ |
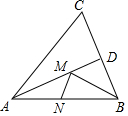如图，在锐角三角形ABC中，AC=6，△ABC的面积为15，∠BAC的平分线交BC与点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是（ ）
17．下列各组数中，互为相反数的是（ ）
| A． | -（+7）和+（-7） | B． | -（-7）与7 | C． | -|-1$\frac{1}{5}$|与-（-$\frac{6}{5}$） | D． | +（-$\frac{1}{100}$）与+（-0.01） |
如图，O是△ABC的∠ABC、∠ACB的角平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若BC=12cm，求△ODE周长．