题目内容
16. 如图,正方形的边长为1dm,剪去四个角后成为一个正八边形.求这个正八边形的边长和面积.
如图,正方形的边长为1dm,剪去四个角后成为一个正八边形.求这个正八边形的边长和面积.
分析 设正八边形的边长为x,根据等腰直角三角形的性质表示出被剪掉的小直角三角形的直角边,然后根据正方形的边长列方程求出x的值,再求出被剪掉的小直角三角形的直角边,最后根据正八边形的面积等于正方形的面积减去四个小直角三角形的面积列式计算即可得解.
解答 解:设正八边形的边长为x,则被剪掉小直角三角形的直角边为$\frac{\sqrt{2}}{2}$x,
由题意得,x+2×$\frac{\sqrt{2}}{2}$x=1,
解得x=$\sqrt{2}$-1,
所以,小直角三角形的直角边为$\frac{\sqrt{2}}{2}$($\sqrt{2}$-1)=1-$\frac{\sqrt{2}}{2}$,
所以,正八边形的面积=12-4×$\frac{1}{2}$×(1-$\frac{\sqrt{2}}{2}$)2=1-2×($\frac{3}{2}$-$\sqrt{2}$)=2$\sqrt{2}$-2.
答:这个正八边形的边长为$\sqrt{2}$-1,面积为2$\sqrt{2}$-2.
点评 本题考查了正多边形和圆,等腰直角三角形的性质,用正八边形的边长表示出等腰直角三角形的直角边是解题的关键,难点在于根据正方形的边长列出方程.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
6.下列图形中,不具有稳定性的是( )
| A. |  | B. |  | C. |  | D. |  |
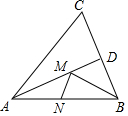 如图,在锐角三角形ABC中,AC=6,△ABC的面积为15,∠BAC的平分线交BC与点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
如图,在锐角三角形ABC中,AC=6,△ABC的面积为15,∠BAC的平分线交BC与点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ) 如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=12cm,求△ODE周长.
如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=12cm,求△ODE周长.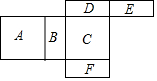 如图是一长方体的展开图,每一面内都标注了字(标字母的面是外表面),根据要求回答问题:如果D面在多面体的左面,那么F面在哪里?
如图是一长方体的展开图,每一面内都标注了字(标字母的面是外表面),根据要求回答问题:如果D面在多面体的左面,那么F面在哪里?