题目内容
9.(1)解方程:x2+4x-1=0;(2)解不等式组$\left\{\begin{array}{l}{1+x≥0}\\{\frac{x}{3}+1>\frac{x+1}{2}}\end{array}\right.$.
分析 (1)用配方法解一元二次方程的步骤:①把原方程化为ax2+bx+c=0(a≠0)的形式;②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;③方程两边同时加上一次项系数一半的平方;④把左边配成一个完全平方式,右边化为一个常数;⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.
(2)先求出不等式组中每一个不等式的解集,再求出它们的公共部分即可得解.
解答 解:(1)x2+4x-1=0,
x2+4x=1,
x2+4x+4=1+4,
(x+2)2=5,
x+2=±$\sqrt{5}$,
x=-2±$\sqrt{5}$;
(2)$\left\{\begin{array}{l}{1+x≥0①}\\{\frac{x}{3}+1>\frac{x+1}{2}②}\end{array}\right.$
解不等式①得:x≥-1,
解不等式②得:x<3.
所以,不等式组的解集是:-1≤x<3.
点评 考查了一元一次不等式组,一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.同时考查了解一元二次方程-配方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
表一
已知甲平时成绩的平均分是98分,乙平时成绩的众数是93分,请你完成下列问题:
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
(3)学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,如果总评成绩不少以90分,平时成绩的平均分和期中成绩不变,那么,这两名学生的期末成绩至少应是多少?
表一
| 测试 类别 | 平时成绩 | 期中 | 期末 | ||||
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | |||
| 甲 | m | 99 | 100 | 99 | 98 | 96 | 95 |
| 乙 | 90 | 93 | 94 | n | 95 | 92 | 98 |
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
| 学生 | 平均数 | 中位数 | 众数 | 方差 |
| 甲 | 98 | 99 | 99 | 4.4 |
| 乙 | 93 | 93 | 93 | 2.8 |
4. 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )
 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )| A. | ∠2+∠3=180° | B. | ∠1=∠4 | C. | ∠2+∠4=180° | D. | ∠2=∠3 |
14.已知抛物线y=x2+bx+c的对称轴为x=1,若关于x的一元二次方程x2-bx-c=0在-3<x<2的范围内有解,则c的取值范围是( )
| A. | c≥-1 | B. | -1≤c<3 | C. | 3<c<8 | D. | -1≤c<8 |
18.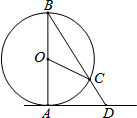 如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
 如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
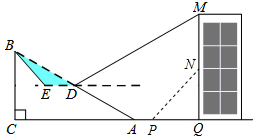 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.