题目内容
20.表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)表一
| 测试 类别 | 平时成绩 | 期中 | 期末 | ||||
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | |||
| 甲 | m | 99 | 100 | 99 | 98 | 96 | 95 |
| 乙 | 90 | 93 | 94 | n | 95 | 92 | 98 |
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
| 学生 | 平均数 | 中位数 | 众数 | 方差 |
| 甲 | 98 | 99 | 99 | 4.4 |
| 乙 | 93 | 93 | 93 | 2.8 |
分析 (1)根据平均数的计算公式求出m的值;再根据众数的定义即可求出n的值;
(2)根据平均数,中位数、众数和方差的计算公式分别进行计算即可;
(3)设甲学生的期末成绩至少应是x分,乙学生的期末成绩至少应是y分,根据平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,列出不等式求解即可.
解答 解:(1)m=98×5-99-100-99-98=94(分),
∵乙平时成绩的众数是93分,
∴n=93分;
(2)根据(1)得:甲的平均数是98,
把甲的成绩从小到大排列,最中间的数是99,则中位数是99;
99出现了2次,出现的次数最多,则众数是99,
甲的方差是:$\frac{1}{5}$[(94-98)2+(99-98)2+(100-98)2+(99-98)2+(98-98)2]=4.4.
乙的平均数是(90+93+94+93+95)÷5=93,
把乙的成绩从小到大排列,最中间的数是93,则中位数是93;
93出现了2次,出现的次数最多,则众数是93,
乙的方差是:$\frac{1}{5}$[(90-93)2+(93-93)2+(94-93)2+(93-93)2+(95-93)2]=2.8.
故答案为:98,99,99,4.4;93,93,93,2.8;
(3)设甲学生的期末成绩至少应是x分,根据题意得:
98×40%+96×20%+40%x≥90,
解得:x≥79,
设乙学生的期末成绩至少应是y分,根据题意得:
93×40%+92×20%+40%y≥90,
解得:y≥86.
答:甲学生的期末成绩至少应是79分,乙学生的期末成绩至少应是86分.
点评 本题考查了众数、中位数、方差,平均数平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.

 阅读快车系列答案
阅读快车系列答案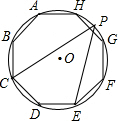 如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )| A. | 30° | B. | 15° | C. | 60° | D. | 45° |
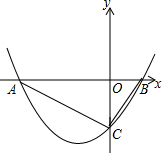 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.