题目内容
13.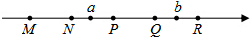 如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )
如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )| A. | M或Q | B. | P或R | C. | N或R | D. | P或Q |
分析 先利用数轴特点确定a,b的关系从而求出a,b的值,确定原点.
解答 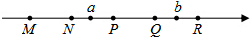 解:∵MN=NP=PQ=QR=1,
解:∵MN=NP=PQ=QR=1,
∴|MN|=|NP|=|PQ|=|QR|=1,
∴|MR|=4;
①当原点在N或P点时,|a|+|b|<3,又因为|a|+|b|=3,所以,原点不可能在N或P点;
②当原点在N或R时且|Na|=|bR|时,|a|+|b|=3;
③当原点在M点时,|a|+|b|>3,又因为|a|+|b|=3,所以,原点不可能在M点;
综上所述,此原点应是在N或R点.
故选:C.
点评 此题主要考查了数轴的定义和绝对值的意义.解此类题的关键是:先利用条件判断出绝对值符号里代数式的正负性,再根据绝对值的性质把绝对值符号去掉,把式子化简后根据整点的特点求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.等式$\frac{1-3x}{\frac{2}{3}}$-3=2x的下列变形属于等式基本性质2变形的是( )
| A. | $\frac{1-3x}{2}$-3=2x+3 | B. | $\frac{3(1-3x)}{2}$-3=2x | C. | 3(1-3x)-6=4x | D. | 3(1-3x)-4x=6 |
3.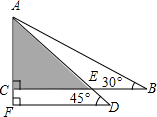 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.| A. | 14 | B. | 24.5 | C. | 7 | D. | 49 |