题目内容
3.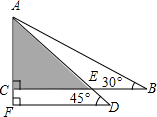 将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.
将一副三角尺如图所示叠放在一起,若AB=14cm,则阴影部分的面积( )cm2.| A. | 14 | B. | 24.5 | C. | 7 | D. | 49 |
分析 由于BC∥DF,那么△ACE也是等腰直角三角形,欲求其面积,必须先求出直角边AC的长;Rt△ABC中,已知斜边AB及∠B的度数,易求得AC的长,进而可根据三角形面积的计算方法求出阴影部分的面积.
解答 解:∵在Rt△ABC中,∠B=30°,∠ACB=90°,AB=14cm,
∴AC=7cm.
∵∠ACB=∠F=90°,
∴BC∥DF,
∴∠AEC=∠ADF=45°,
∴AC=CE=7cm.
故S△ACE=$\frac{1}{2}$×7×7=24.5(cm2).
故选B.
点评 本题考查了解直角三角形,发现△ACE是等腰直角三角形,并能根据直角三角形的性质求出直角边AC的长,是解答此题的关键.

练习册系列答案
相关题目
13.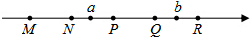 如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )
如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )
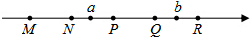 如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )
如图,M,N,P,Q,R分别是数轴上五个整数所对应的点,其中有一点是原点,并且MN=NP=PQ=QR=1.数a对应的点在N与P之间,数b对应的点在Q与R之间,若|a|+|b|=3,则原点可能是( )| A. | M或Q | B. | P或R | C. | N或R | D. | P或Q |
12. 如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )
如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )
 如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )
如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )| A. | P是BC中点 | B. | ∠APE=90° | C. | ∠APB=∠EPC | D. | BP:BC=2:3 |
 数轴上A、B、C、D四个点表示的数分别为:A-3;B-1;C1;D3.
数轴上A、B、C、D四个点表示的数分别为:A-3;B-1;C1;D3. 如图,在△ABC中,∠ADE=∠C,AE=3,AB=6,AD=2.4,则AC=4.8.
如图,在△ABC中,∠ADE=∠C,AE=3,AB=6,AD=2.4,则AC=4.8.