题目内容
11.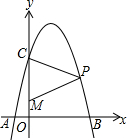 如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3).
如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3).
分析 作PD⊥y轴D,根据等腰三角形的性质得出CD=MD,进而根据C、M的坐标求得D的坐标,即可求得P的纵坐标,代入解析式即可求得P的坐标.
解答  解:作PD⊥y轴D,
解:作PD⊥y轴D,
∵△PCM是以CM为底的等腰三角形,
∴CD=MD,
∵抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C,
∴C(0,5),
∵M(0,1),
∴CM=5-1=4,
∴CD=2,
∴OD=5-2=3,
∴D(0,3),
把y=3代入y=-x2+4x+5得,3=-x2+4x+5,
解得x=2±$\sqrt{6}$
∴P(2+$\sqrt{6}$,3).
故答案为(2+$\sqrt{6}$,3).
点评 本题考查了抛物线与y轴的交点,等腰三角形的性质以及二次函数图象上点的坐标特征,求得P点的纵坐标是关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
2. 如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
 如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )
如图,在平面直角坐标系中,⊙O的半径为2,AC,BD是⊙O的两条互相垂直的弦,垂足为M(1,$\sqrt{2}$),则四边形ABCD面积最大值为( )| A. | 2$\sqrt{6}$ | B. | 5 | C. | 4 | D. | 6 |
19.下列计算正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 32=6 | C. | (-1)2015=-1 | D. | |-2|=-2 |
3.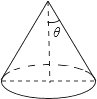 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
 已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )
已知圆锥的底面半径为3cm,侧面积为15πcm2,设圆锥的母线与高的夹角为θ(如图所示),则tanθ的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
20.一个边长为a的正方形,若将其边长增加6cm,则新的正方形的面积增加( )
| A. | 36cm2 | B. | 12acm2 | C. | (36+12a)cm2 | D. | 以上都不对 |
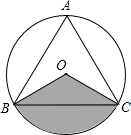 如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.
如图,等边△ABC内接于⊙O,AB=4$\sqrt{3}$.