题目内容
因式分解: 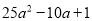 =______________
=______________
 【解析】根据完全平方公式进行因式分解为: =.
故答案为: .
【解析】根据完全平方公式进行因式分解为: =.
故答案为: .
练习册系列答案
相关题目
如果关于x的不等式|x﹣2|+|x+3|≥a对于x取任意数都成立,则a的取值范围是多少?并说明理由.
 a≤5
【解析】试题分析:根据线段上的点到线两端点的距离的和最小,可得答案.
试题分析:∵|x﹣2|+|x+3|≥5,
∴关于x的不等式|x﹣2|+|x+3|≥a对于x取任意数都成立,
a≤5.
a≤5
【解析】试题分析:根据线段上的点到线两端点的距离的和最小,可得答案.
试题分析:∵|x﹣2|+|x+3|≥5,
∴关于x的不等式|x﹣2|+|x+3|≥a对于x取任意数都成立,
a≤5. 讨论993-99能被100整除吗?
 能
【解析】试题分析:根据提公因式法--因式分解,化为几个因数积的形式,而得到整除的结论.
试题解析:993-99
=99×992-99
=99×(992-1)
=99×9800
=99×98×100
其中有一个因数为100,所以993-99能被100整除.
能
【解析】试题分析:根据提公因式法--因式分解,化为几个因数积的形式,而得到整除的结论.
试题解析:993-99
=99×992-99
=99×(992-1)
=99×9800
=99×98×100
其中有一个因数为100,所以993-99能被100整除. 下列各式从左到右的变形中,是用公式法分解因式的是( )
A. 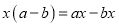 B.
B. 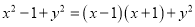
C. 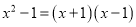 D.
D. 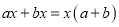
 C
【解析】根据平方差公式: ,完全平方公式: ,可知C选项的分解因式的方法是平方差公式,D选项是利用提公因式法分解因式,A、B不是分解因式.
故选:C.
C
【解析】根据平方差公式: ,完全平方公式: ,可知C选项的分解因式的方法是平方差公式,D选项是利用提公因式法分解因式,A、B不是分解因式.
故选:C. 在公式法分解因式中,有一种公式a3+b3=(a+b)(a2-ab+b2)叫立方和公式,请用它把x3+8分解因式
 (x+2)·(x2-2x+4)
【解析】试题分析:根据所给公式,将x3+8先变形为x3+23,然后套用公式,进行分解即可.
试题解析:x3+8=x3+23=(x+2)·(x2-2x+4)
(x+2)·(x2-2x+4)
【解析】试题分析:根据所给公式,将x3+8先变形为x3+23,然后套用公式,进行分解即可.
试题解析:x3+8=x3+23=(x+2)·(x2-2x+4) 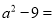 _________
_________
 【解析】根据平方差公式: ,可因式分解为: .
故答案为: .
【解析】根据平方差公式: ,可因式分解为: .
故答案为: . 下列多项式不能用公式法分解因式的是( )
A. 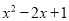 B.
B. 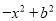 C.
C. 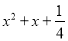 D.
D. 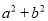
 D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D.
D
【解析】根据平方差公式: ,完全平方公式: 的特点,可知:A、B、C选项可以利用完全平方公式和平方差公式进行分解因式,D选项不能利用公式法分解因式.
故选:D. 已知:如图,AC=CD ,∠B=∠E=90°, AC⊥CD,则不正确的结论是 ( )
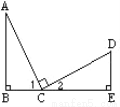
A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△CED D. ∠1=∠2
 D
【解析】∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
,
∴△ABC≌△CED(AAS),
故B、C选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故A选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=...
D
【解析】∵AC⊥CD,
∴∠1+∠2=90°,
∵∠B=90°,
∴∠1+∠A=90°,
∴∠A=∠2,
在△ABC和△CED中,
,
∴△ABC≌△CED(AAS),
故B、C选项正确;
∵∠2+∠D=90°,
∴∠A+∠D=90°,
故A选项正确;
∵AC⊥CD,
∴∠ACD=90°,
∠1+∠2=... 因为-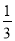 x>1,所以x____-3(填“>”或“<”),依据是__________________.
x>1,所以x____-3(填“>”或“<”),依据是__________________.
 < 不等式的基本性质3
【解析】不等式两边同时乘以-3得,x<-3,
故答案为:<,不等式的基本性质3.
< 不等式的基本性质3
【解析】不等式两边同时乘以-3得,x<-3,
故答案为:<,不等式的基本性质3. 
