题目内容
1.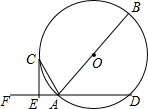 如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
分析 (1)证明:连接CO,证得∠OCA=∠CAE,由平行线的判定得到OC∥FD,再证得OC⊥CE,即可证得结论;
(2)证明:连接BC,由圆周角定理得到∠BCA=90°,再证得△ABC∽△ACE,根据相似三角形的性质即可证得结论.
解答 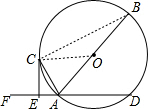 (1)证明:连接CO,
(1)证明:连接CO,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠FAB,
∴∠OCA=∠CAE,
∴OC∥FD,
∵CE⊥DF,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)证明:连接BC,
在Rt△ACE中,AC=$\sqrt{A{E}^{2}+E{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{1}}$=$\sqrt{5}$,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠BCA=∠CEA,
∵∠CAE=∠CAB,
∴△ABC∽△ACE,
∴$\frac{CA}{AB}$=$\frac{AE}{AC}$,
∴$\frac{\sqrt{5}}{AB}=\frac{1}{\sqrt{5}}$,
∴AB=5,
∴AO=2.5,即⊙O的半径为2.5.
点评 本题主要考查了圆周角定理,切线的判定,平行线的性质和判定,勾股定理,相似三角形的判定和性质,熟练掌握切线的判定定理是解决问题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
11. 如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
 如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )
如图,矩形ABCD与菱形EFGH的对角线均交于点O,且EG∥BC,将矩形折叠,使点C与点O重合,折痕MN恰好过点G若AB=$\sqrt{6}$,EF=2,∠H=120°,则DN的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{3}}{2}$ | C. | $\sqrt{6}$-$\sqrt{3}$ | D. | 2$\sqrt{3}$-$\sqrt{6}$ |
12.宽与长的比是$\frac{\sqrt{5}-1}{2}$(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD、BC的中点E、F,连接EF:以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是( )
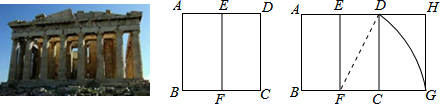

| A. | 矩形ABFE | B. | 矩形EFCD | C. | 矩形EFGH | D. | 矩形DCGH |
9.若关于x的一元二次方程x2-3x+p=0(p≠0)的两个不相等的实数根分别为a和b,且a2-ab+b2=18,则$\frac{a}{b}$+$\frac{b}{a}$的值是( )
| A. | 3 | B. | -3 | C. | 5 | D. | -5 |
16. 在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
请结合图表中的信息解答下列问题:
(1)统计表中,a=15,b=0.3;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为72°;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有300株.
 在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:“宇番2号”番茄挂果数量统计表
| 挂果数量x(个) | 频数(株) | 频率 |
| 25≤x<35 | 6 | 0.1 |
| 35≤x<45 | 12 | 0.2 |
| 45≤x<55 | a | 0.25 |
| 55≤x<65 | 18 | b |
| 65≤x<75 | 9 | 0.15 |
(1)统计表中,a=15,b=0.3;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为72°;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有300株.
13. 如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )
如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )
 如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )
如图,直线a∥b,∠1=85°,∠2=35°,则∠3=( )| A. | 85° | B. | 60° | C. | 50° | D. | 35° |
 如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)
如图,已知△ABC,∠BAC=90°,请用尺规过点A作一条直线,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法)