��Ŀ����
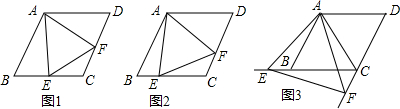
12�����볤�ı���$\frac{\sqrt{5}-1}{2}$��Լ0.618���ľ��ν����ƽ���Σ��ƽ�����̲��ŷḻ����ѧ��ֵ����������Э�����ȳƵ����У����ǿ����������ķ��������ƽ���Σ���������ABCD���ֱ�ȡAD��BC���е�E��F������EF���Ե�FΪԲ�ģ���FDΪ�뾶��������BC���ӳ����ڵ�G����GH��AD����AD���ӳ����ڵ�H����ͼ�����о����ǻƽ���ε��ǣ�������
| A�� | ����ABFE | B�� | ����EFCD | C�� | ����EFGH | D�� | ����DCGH |
���� �ȸ��������ε������Լ����ɶ��������DF�ij����ٸ���DF=GF���CG�ij���������CG��CD�ı�ֵΪ�ƽ�ȣ��жϾ���DCGHΪ�ƽ���Σ�
��� �⣺�������εı߳�Ϊ2����CD=2��CF=1
��ֱ��������DCF�У�DF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$
��FG=$\sqrt{5}$
��CG=$\sqrt{5}$-1
��$\frac{CG}{CD}$=$\frac{\sqrt{5}-1}{2}$
�����DCGHΪ�ƽ����
��ѡD��
���� ������Ҫ�����˻ƽ�ָ�������Ĺؼ������ջƽ���εĸ������ʱע�⣬���볤�ı���$\frac{\sqrt{5}-1}{2}$�ľ��ν����ƽ���Σ�ͼ�еľ���ABGHҲΪ�ƽ���Σ�

��ϰ��ϵ�д�
 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
�����Ŀ
2������ʽ���У���ȷ���ǣ�������
| A�� | a2•a3=a6 | B�� | ��3ab2��3=9a3b6 | C�� | ��a2b��3�£�-ab��2=a4b | D�� | ��a-2��2=a2-4 |
3��$\sqrt{9}$=��������
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
20������������ȷ���ǣ�������
| A�� | 3+$\sqrt{3}$=3$\sqrt{3}$ | B�� | $\sqrt{{{��-2��}^2}}$=2 | C�� | $\sqrt{50}$=$\sqrt{25+25}$=5+5=10 | D�� | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ |
17��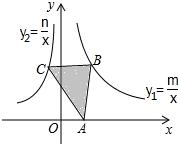 ��ͼ����֪��ABC����A��x���ϣ���B��˫����y1=$\frac{m}{x}$��m��0��x��0���ϣ���C��˫����y2=$\frac{n}{x}$��n��0��x��0���ϣ����ڡ�ABC�����������˵������ȷ���ǣ�������
��ͼ����֪��ABC����A��x���ϣ���B��˫����y1=$\frac{m}{x}$��m��0��x��0���ϣ���C��˫����y2=$\frac{n}{x}$��n��0��x��0���ϣ����ڡ�ABC�����������˵������ȷ���ǣ�������
 ��ͼ����֪��ABC����A��x���ϣ���B��˫����y1=$\frac{m}{x}$��m��0��x��0���ϣ���C��˫����y2=$\frac{n}{x}$��n��0��x��0���ϣ����ڡ�ABC�����������˵������ȷ���ǣ�������
��ͼ����֪��ABC����A��x���ϣ���B��˫����y1=$\frac{m}{x}$��m��0��x��0���ϣ���C��˫����y2=$\frac{n}{x}$��n��0��x��0���ϣ����ڡ�ABC�����������˵������ȷ���ǣ�������| A�� | ����A���ֲ�������C��B�����ƶ�ʱ����ABC��������� | |
| B�� | ����A�ƶ���BC���ֲ���ʱ����ABC��������� | |
| C�� | ���ܵ�A��B��C��ô�ƶ�����ABC�����ʼ�ղ��� | |
| D�� | ���ܵ�A��B��C��ô�ƶ���ֻҪBC��x��ƽ�У���ABC������Ͳ��� |
 ƽ���ı���ABCD����������A��C�ڷ���������y=$\frac{k}{x}$��k��0��ͼ���ϣ���B��D��x���ϣ���B��D�������ԭ��Գƣ�AD��y����P��
ƽ���ı���ABCD����������A��C�ڷ���������y=$\frac{k}{x}$��k��0��ͼ���ϣ���B��D��x���ϣ���B��D�������ԭ��Գƣ�AD��y����P��
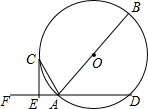 ��ͼ��AB�ǡ�O��ֱ����AD�ǡ�O���ң���F��DA�ӳ��ߵ�һ�㣬ACƽ�֡�FAB����O�ڵ�C������C��CE��DF������Ϊ��E��
��ͼ��AB�ǡ�O��ֱ����AD�ǡ�O���ң���F��DA�ӳ��ߵ�һ�㣬ACƽ�֡�FAB����O�ڵ�C������C��CE��DF������Ϊ��E��