题目内容
17. 完成下面的证明过程:
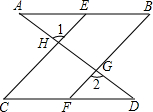
完成下面的证明过程:如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB(对顶角相等)
∴∠1=∠AGB(等量代换)
∴EC∥BF(同位角相等,两直线平行)
∴∠B=∠AEC(两直线平行,同位角相等)
又∵∠B=∠C(已知)
∴∠AEC=∠C(等量代换)
∴AB∥CD(内错角相等,两直线平行)
∴∠A=∠D(两直线平行,内错角相等)
分析 求出∠1=∠AGB,根据平行线的判定得出EC∥BF,根据平行线的性质得出∠B=∠AEC,求出∠AEC=∠C,根据平行线的判定得出AB∥CD即可.
解答 证明:∵∠1=∠2,(已知)∠2=∠AGB(对顶角相等)
∴∠1=∠AGB(等量代换),
∴EC∥BF(同位角相等,两直线平行)
∴∠B=∠AEC(两直线平行,同位角相等),
又∵∠B=∠C(已知)
∴∠AEC=∠C(等量代换)
∴AB∥CD(内错角相等,两直线平行),
∴∠A=∠D(两直线平行,内错角相等),
故答案为:对顶角相等,∠AGB,等量代换,同位角相等,两直线平行,两直线平行,同位角相等,∠C,等量代换,AB∥CD,内错角相等,两直线平行,两直线平行,内错角相等.
点评 本题考查了平行线的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
8.按下列程序计算,把答案填写在表格内,并观察有什么规律,想想为什么有这样的规律?

(1)填写表内空格:
(2)发现的规律是:(用含x的式子表示)(x2+2x)÷x-1=x+1.

(1)填写表内空格:
| 输入x | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | … |
| 输出答案 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | $\frac{2}{3}$ | … |
 如图,Rt△ABC中,∠C=90°,D是AB的中点,若AB=10,则CD的长等于5.
如图,Rt△ABC中,∠C=90°,D是AB的中点,若AB=10,则CD的长等于5.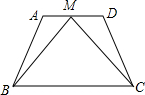 已知:如图,AB=CD,∠A=∠D,点M是AD的中点.
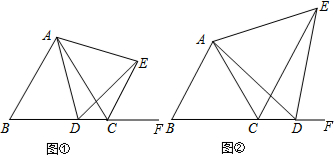
已知:如图,AB=CD,∠A=∠D,点M是AD的中点. 如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是65°.
如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是65°.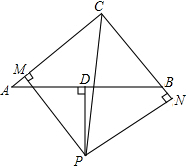 如图,在△ABC中,D是AB边的中点,PD⊥AB交∠ACB的平分线与点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N.
如图,在△ABC中,D是AB边的中点,PD⊥AB交∠ACB的平分线与点P,PM⊥AC于点M,PN⊥BC交CB的延长线于点N.