题目内容
5.已知等边△ABC,点D是直线BC上一点,以AD为边在AD的右侧作等边△ADE,连结CE.(1)如图①,若点D在线段BC上,求证:CE+CD=AB;
(2)如图②,若点D在BC延长线上,线段CD,CE和AB有怎样的数量关系?证明你的结论.
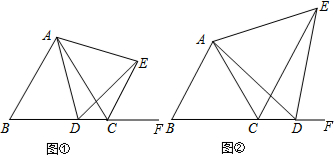
分析 (1)如图①,根据△ADE与△ABC都是等边三角形,容易得到全等条件证明△CAE≌△BAD,再根据全等三角形的性质可以证明题目的结论;
(2)如图②,根据(1)可知D的位置对△CAE≌△BAD没有影响,所以BD=CE,所以CE-CD=AB,证明方法与(1)相同.
解答 证明:(1)如图①,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE-∠CAD=∠BAC-∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$,
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE+CD=DB+CD=BC=AB,
即CE+CD=AB;
(2)CE-CD=AB;
理由如下:如图②,∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°.
∴∠DAE+∠CAD=∠BAC+∠CAD.
即∠CAE=∠BAD.
在△CAE和△BAD中,
$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAD}\\{AE=AD}\end{array}\right.$,
∴△CAE≌△BAD(SAS).
∴EC=DB(全等三角形的对应边相等);
∴CE-AB=DB-BC=CD,即CE-CD=AB.
点评 本题主要考查了等边三角形的性质、全等三角形的判定与性质以及类比思想的运用.发现全等三角形是解决问题的关键.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | -8-3=-5 | B. | 0-(-6)=-6 | C. | -23=-8 | D. | 7÷$\frac{1}{7}$×7=7 |
10.如果等腰直角三角形的两边长为2cm,4cm,那么它的周长为( )
| A. | 8cm | B. | 10cm | C. | 11cm | D. | 8cm或10cm |
14.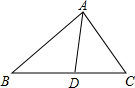 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=( )| A. | 3:4 | B. | 4:3 | C. | 16:9 | D. | 9:16 |
 在四边形ABDC中,AB=AC,∠B=∠C,BD=10,则DC=10.
在四边形ABDC中,AB=AC,∠B=∠C,BD=10,则DC=10.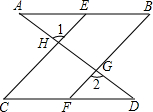 完成下面的证明过程:
完成下面的证明过程: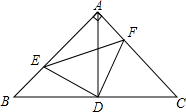 如图,在△ABC中,∠A=90°,AB=AC,D 是BC的中点,点E、F分别是AB,AC上的点,并且BE=AF
如图,在△ABC中,∠A=90°,AB=AC,D 是BC的中点,点E、F分别是AB,AC上的点,并且BE=AF