题目内容
9.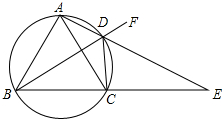 如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.
如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,AB=AC.(1)求证:DE平分∠CDF;
(2)求证:∠ACD=∠AEB.
分析 (1)根据圆内接四边形的性质得到∠CDE=∠ABC,根据圆周角定理和等腰三角形的性质证明即可;
(2)根据三角形外角的性质和图形得到∠CAE+∠E=∠ABD+∠DBC,得到∠E=∠ABD,根据圆周角定理证明.
解答 (1)证明:∵四边形ABCD内接于圆,
∴∠CDE=∠ABC,
由圆周角定理得,∠ACB=∠ADB,又∠ADB=∠FDE,
∴∠ACB=∠FDE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FDE=∠CDE,即DE平分∠CDF;
(2)∵∠ACB=∠ABC,
∴∠CAE+∠E=∠ABD+∠DBC,
又∠CAE=∠DBC,
∴∠E=∠ABD,
∴∠ACD=∠AEB.
点评 本题考查的是圆内接四边形的性质、等腰三角形的性质以及三角形外角的性质,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.甲、乙两名同学在周长为400m的环形跑道上训练跑步,甲在乙前边100m,两人同时背相出发,经过25s第一次相遇;两人同时同向出发,经过50s第一次相遇,已知甲比乙跑得慢,设甲每秒跑xm,乙每秒跑ym,则可列出的方程组为( )
| A. | $\left\{\begin{array}{l}{25(x+y)=400-100}\\{50(y-x)=400+100}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{25(x+y)=400}\\{50(y-x)=100}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{25(x+y)=400-100}\\{50(y-x)=400}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{25(x+y)=400-100}\\{50(y-x)=100}\end{array}\right.$ |