题目内容
11.“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如表:| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(Ⅰ)当x为何值时,购进这两种文具的进货款恰好为1320元;
(Ⅱ)当x为何值时,销售这批文具所获利润最大,并且所获利润不超过进货价格的40%,最大利润是多少元.
分析 (Ⅰ)根据题意可以列出相应的方程,从而可以解答本题;
(Ⅱ)根据题意可以得到利润与x的关系式,然后根据所获利润不超过进货价格的40%,列出相应的不等式,从而可以求得最大利润.
解答 解:(Ⅰ)由题意可得,
10x+15(100-x)=1320,
解得,x=36
即x=36时,购进这两种文具的进货款恰好为1320元;
(Ⅱ)设利润为w元,
w=(12-10)x+(23-15)(100-x)=800-6x,
∵所获利润不超过进货价格的40%,
∴800-6x≤40%[10x+15(100-x)]
解得,x≥50
∴当x=50时,w取得最大值,此时w=800-6×50=500,
即当x=50时,销售这批文具所获利润最大,并且所获利润不超过进货价格的40%,最大利润是500元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和不等式的相关知识解答.

练习册系列答案
相关题目
3.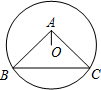 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
20.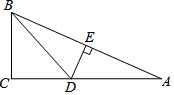 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )
 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |

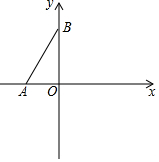 如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.
如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°. 猴年到了,申申设计了一个电子猴游戏,让电子猴在一个边长为1个单位长度的正六边形的顶点上跳动(如图.),游戏者通过摸球来确定电子猴的走法,规则是:在不透明的袋 子里装有3个标号分别为2,3,4的质地、大小相同的小球,搅匀后任意摸出一个,记下 标号后放回袋中并搅匀,再从中任意摸出一个,摸出的两个小球标号的和是几,电子猴就 从点A按顺时针方向沿边依次跳动几个单位长度.
猴年到了,申申设计了一个电子猴游戏,让电子猴在一个边长为1个单位长度的正六边形的顶点上跳动(如图.),游戏者通过摸球来确定电子猴的走法,规则是:在不透明的袋 子里装有3个标号分别为2,3,4的质地、大小相同的小球,搅匀后任意摸出一个,记下 标号后放回袋中并搅匀,再从中任意摸出一个,摸出的两个小球标号的和是几,电子猴就 从点A按顺时针方向沿边依次跳动几个单位长度.