题目内容
20．
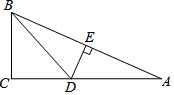如图，在Rt△ABC中，∠C=90°，把AB对折后，点A与点B重合，折痕为DE，若BC=2，AC=4，则BD=（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |
分析 根据翻折的性质可得BD=AD，设BD=x，表示出CD，然后利用勾股定理列方程求解即可．
解答 解：∵把AB对折后，点A与点B重合，折痕为DE，
∴BD=AD，
设BD=x，则CD=AC-AD=4-x，
∵∠C=90°，
∴BC2+CD2=BD2，
即22+（4-x）2=x2，
解得x=$\frac{5}{2}$，
即BD=$\frac{5}{2}$．
故选C．
点评 本题考查了翻折变换的性质，勾股定理，主要利用了翻折前后对应边相等，此类题目，利用勾股定理列出方程是解题的关键．
练习册系列答案
相关题目
11．“六一”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如表：
设小张购进A型文具x只．
（Ⅰ）当x为何值时，购进这两种文具的进货款恰好为1320元；
（Ⅱ）当x为何值时，销售这批文具所获利润最大，并且所获利润不超过进货价格的40%，最大利润是多少元．
| 型号 | 进价（元/只） | 售价（元/只） |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
（Ⅰ）当x为何值时，购进这两种文具的进货款恰好为1320元；
（Ⅱ）当x为何值时，销售这批文具所获利润最大，并且所获利润不超过进货价格的40%，最大利润是多少元．
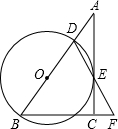如图，在 Rt△ABC中，∠ACB=90°，点D是边AB上一点，以BD为直径的⊙O与边AC相切于点E，连接DE并延长DE交BC的延长线于点F．
5．
有理数a，b在数轴上的位置如图所示，则|a+b|+|a-b|化简的结果为（ ）
有理数a，b在数轴上的位置如图所示，则|a+b|+|a-b|化简的结果为（ ）| A． | -2b | B． | -2a | C． | 2b | D． | 0 |
用一平面去截一个正方体，能截出梯形，请在如图的正方体中画出．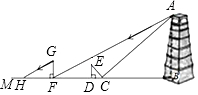
如图，小亮、小芳同学想测量一座塔的高度，他们经过观察发现需要两次测量，于是他们首先用平面镜进行测量，方法如下：如图，小芳在小亮和塔之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小亮看着镜面上的标记，来回走动，走到点D时，看到塔顶端点A在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度ED=1.5米，CD=3米；然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从D点沿DM方向走了17米，到达塔影子的末端F点处，此时，测得小亮身高GF的影长FH=4.2米，GF=1.6米，如图，已知AB⊥BM，ED⊥BM，GF⊥CM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中的信息，求出塔的高AB的长度．