题目内容
3.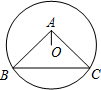 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
分析 过O作OD⊥BC,由垂径定理可知BD=CD=$\frac{1}{2}$BC,根据△ABC是等腰直角三角形可知∠ABC=45°,故△ABD也是等腰直角三角形,BD=AD,再由OA=1可求出OD的长,在Rt△OBD中利用勾股定理即可求出OB的长.
解答 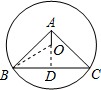 解:过O作OD⊥BC,
解:过O作OD⊥BC,
∵BC是⊙O的一条弦,且BC=6,
∴BD=CD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3,
∴OD垂直平分BC,又AB=AC,
∴点A在BC的垂直平分线上,即A,O及D三点共线,
∵△ABC是等腰直角三角形,
∴∠ABC=45°,
∴△ABD也是等腰直角三角形,
∴AD=BD=3,
∵OA=1,
∴OD=AD-OA=3-1=2,
在Rt△OBD中,
OB=$\sqrt{B{D}^{2}+O{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
故选C.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
11.“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如表:
设小张购进A型文具x只.
(Ⅰ)当x为何值时,购进这两种文具的进货款恰好为1320元;
(Ⅱ)当x为何值时,销售这批文具所获利润最大,并且所获利润不超过进货价格的40%,最大利润是多少元.
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(Ⅰ)当x为何值时,购进这两种文具的进货款恰好为1320元;
(Ⅱ)当x为何值时,销售这批文具所获利润最大,并且所获利润不超过进货价格的40%,最大利润是多少元.
13.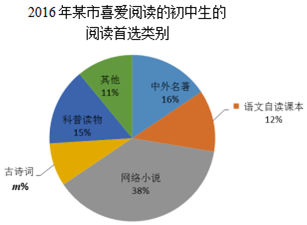 某城市2016年约有初中生10万人,2017年初中生人数还会略有增长.该市青少年活动中心对初中生阅读情况进行了统计,绘制的统计图表如表:
某城市2016年约有初中生10万人,2017年初中生人数还会略有增长.该市青少年活动中心对初中生阅读情况进行了统计,绘制的统计图表如表:
2013-2016年某市喜爱阅读的初中生人数
根据以上信息解答下列问题:
(1)扇形统计图中m的值为8;
(2)2016年,在该市喜爱阅读的初中生中,首选阅读科普读物的人数为0.75万;
(3)请你结合对数据的分析,预估2017年该市喜爱阅读的初中生人数,并简单说明理由.
 某城市2016年约有初中生10万人,2017年初中生人数还会略有增长.该市青少年活动中心对初中生阅读情况进行了统计,绘制的统计图表如表:
某城市2016年约有初中生10万人,2017年初中生人数还会略有增长.该市青少年活动中心对初中生阅读情况进行了统计,绘制的统计图表如表:2013-2016年某市喜爱阅读的初中生人数
| 年份 | 喜爱阅读的初中生人数(万人) |
| 2013 | 1.0 |
| 2014 | 2.2 |
| 2015 | 3.5 |
| 2016 | 5.0 |
(1)扇形统计图中m的值为8;
(2)2016年,在该市喜爱阅读的初中生中,首选阅读科普读物的人数为0.75万;
(3)请你结合对数据的分析,预估2017年该市喜爱阅读的初中生人数,并简单说明理由.
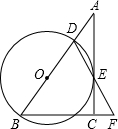 如图,在 Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.
如图,在 Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F. 用一平面去截一个正方体,能截出梯形,请在如图的正方体中画出.
用一平面去截一个正方体,能截出梯形,请在如图的正方体中画出.