题目内容
16.如果n是正整数,求证:3n+2-2n+2+3n-2n能被10整除.分析 首先分组分解,再进一步探讨得出答案即可.
解答 解:∵3n+2-2n+2+3n-2n
=3n+2+3n-2n+2-2n
=3n(32+1)-2n(22+1)
=10×3n-2n-1×10
=10×(3n-2n-1),
∴3n+2-2n+2+3n-2n能被10整除.
点评 此题考查因式分解的实际运用,掌握提取公因式法的方法和同底数幂的乘法是解决问题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
11.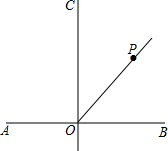 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{\frac{1}{x}+y=4}\\{x-y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+3y=6}\\{2x+y=4}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=4}\\{x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+5y=25}\\{x+10y=25}\end{array}\right.$ |
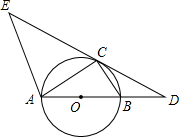 如图,AB是⊙O的直径,点C在⊙O上,∠DCB=∠CAB,AE∥BC,AE交DC的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,∠DCB=∠CAB,AE∥BC,AE交DC的延长线于点E.