题目内容
如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
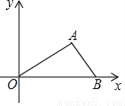
A. 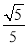 B.
B. 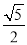 C.
C. 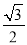 D.
D. 
 A
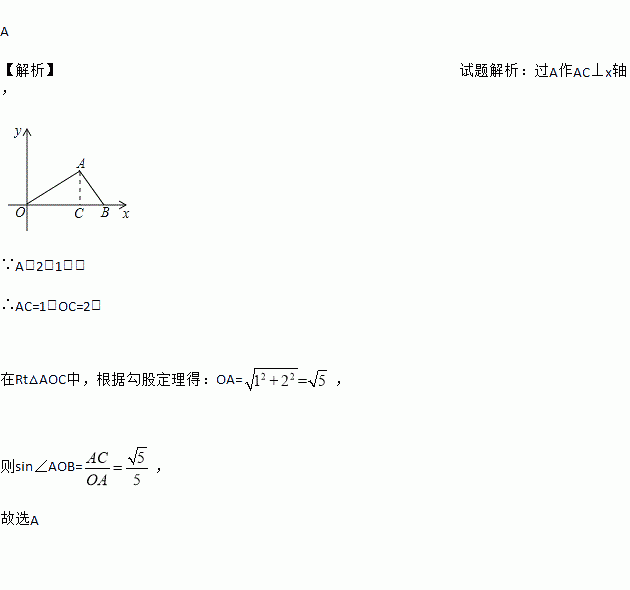
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
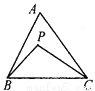
已知:如图,P是△ABC内任一点,求证:AB+AC>BP+PC.
 证明见解析.
【解析】试题分析:延长BP交AC于点D,由三角形的三边关系可得AB+AD>BD,PD+DC>PC,
试题解析:如图,延长BP交AC于点D.
在△ABD中,根据三边关系可得:
∵BD=BP+DP,
∴AB+AD>BP+DP.
在△PCD中,根据三边关系可得:PD+DC>PC,
证明见解析.
【解析】试题分析:延长BP交AC于点D,由三角形的三边关系可得AB+AD>BD,PD+DC>PC,
试题解析:如图,延长BP交AC于点D.
在△ABD中,根据三边关系可得:
∵BD=BP+DP,
∴AB+AD>BP+DP.
在△PCD中,根据三边关系可得:PD+DC>PC, 化简: 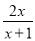 +
+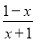 =___.
=___.
 1
【解析】分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可.
解答:【解析】
原式==1.
1
【解析】分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可.
解答:【解析】
原式==1. 在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为: 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
 D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D.
D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D. 在Rt△ABC中,∠C=90°,如果AC:BC=3:4,求cosA的值.
 【解析】分析:根据题意设AC=3x,BC=4x,故AB=5x,进而利用锐角三角函数关系求出答案.
本题解析:
∵在Rt△ABC中,∠C=90°,AC:BC=3:4,
∴设AC=3x,BC=4x,故AB=5x,
则cosA=
故答案为:
【解析】分析:根据题意设AC=3x,BC=4x,故AB=5x,进而利用锐角三角函数关系求出答案.
本题解析:
∵在Rt△ABC中,∠C=90°,AC:BC=3:4,
∴设AC=3x,BC=4x,故AB=5x,
则cosA=
故答案为: 在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cos A的值等于 .
 .
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:.
.
【解析】
试题分析:∵在Rt△ABC中,∠C=90°,AC=4,BC=3,∴AB==,∴cosA==,故答案为:. 近期,大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售,某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当单价从38元/千克下调了x元时,销售量为y千克.
(1)写出y与x之间的关系式;
(2)如果凤梨的进价是20元/千克,某天的销售价定为30元/千克,这天的销售利润是多少?
(3)以前在两岸未直接通航时,运输要绕行,需耗时一周(七天),凤梨最长的保存期为一个月(30天),若每天售价不低于30元/千克,一次进货最多只能是多少千克?
 (1)y=50+2x;(2) 1518千克
【解析】试题分析:(1)根据表格发现每下调一元,多销售2kg,由此即可解决问题.
(2)当x=30时,代入解析式求出销量,根据利润=售价-进价就可以求出结论;
(3)根据凤梨的保存时间和运输路线的影响,凤梨的销售时间最多是23天.要想使售价不低于30元/千克,就必须在最多23天内卖完,当售价为30元/千克时,销售量已经由(2)求出,因此...
(1)y=50+2x;(2) 1518千克
【解析】试题分析:(1)根据表格发现每下调一元,多销售2kg,由此即可解决问题.
(2)当x=30时,代入解析式求出销量,根据利润=售价-进价就可以求出结论;
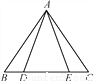
(3)根据凤梨的保存时间和运输路线的影响,凤梨的销售时间最多是23天.要想使售价不低于30元/千克,就必须在最多23天内卖完,当售价为30元/千克时,销售量已经由(2)求出,因此... 如图,点D,E在△ABC的边BC上,AB=AC,BD=CE.
求证:AD=AE.
 证明见解析
【解析】试题分析:利用等腰三角形的性质得到∠B=∠C,然后证明△ABD≌△ACE即可证得结论.
【解答】证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△ACE中,
∵,
∴△ABD≌△ACE(SAS),
∴AD=AE.
证明见解析
【解析】试题分析:利用等腰三角形的性质得到∠B=∠C,然后证明△ABD≌△ACE即可证得结论.
【解答】证明:∵AB=AC,
∴∠B=∠C,
在△ABD与△ACE中,
∵,
∴△ABD≌△ACE(SAS),
∴AD=AE.