题目内容
已知点M(－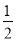
，3m)关于原点对称的点在第一象限，那么m的取值范围是____________.
m<0
【解析】因为点M（,3m）关于原点对称的点在第一象限,所以－3m＞0,所以m＜0,故答案为:m＜0.
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
观察图中的汽车商标，其中是轴对称图形的个数为
A、2 B、3 C、4 D、5
B
【解析】
试题分析：轴对称图形的定义：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
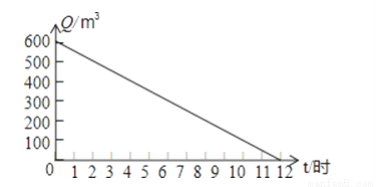
由图可得轴对称图形为第一个、第二个、第四个，故选B. 河道的剩水量Q（米3）和水泵抽水时间t（时）的关系图象如图，则水泵抽水前，河道内有______ 米3的水，水泵最多抽________ 小时，水泵抽8小时后，河道剩水量是________ 米3 ．
600 12 200
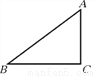
【解析】观察图象可知, 水泵抽水前，河道内有600米3的水，水泵最多抽12小时，水泵抽8小时后，河道剩水量是600－600÷12×8＝200米3． 如图，某河道要建造一座公路桥，要求桥面离地面高度AC为3米，该桥的坡角∠ABC为15°，则该桥的水平距离BC的长是___米(精确到0.1米)．
11.2
【解析】试题解析：Rt△ABC中,
(米).
故答案为：11.2. 求cos42°，下列按键正确的是( )
A. 
B. 
C. D. 
A
【解析】试题解析：用计算器计算一个锐角的三角函数值的步骤，先三角函数，之后度数，最后等号；
故选A. 点P（x，y）关于x轴对称的点P1为______；关于y轴对称的点P2为______；关于原点的对称点P3为______.
（x，-y） （-x，y） （-x，-y）
【解析】点P（x,y）关于x轴对称的点P1为 （x，-y）,关于y轴对称的点P2为 （-x,y）,关于原点的对称点P3为（-x，-y）,故答案为:（x,-y）,（-x,y）,（-x,-y）. 已知：如图，P是△ABC内任一点，求证：AB＋AC＞BP＋PC．
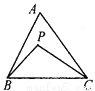
证明见解析.
【解析】试题分析：延长BP交AC于点D，由三角形的三边关系可得AB+AD＞BD，PD+DC＞PC，
试题解析：如图，延长BP交AC于点D.
在△ABD中，根据三边关系可得：
∵BD=BP+DP，
∴AB+AD＞BP+DP.
在△PCD中，根据三边关系可得：PD+DC＞PC， 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________．
37cm
【解析】①7cm是腰长时，三角形的三边分别为7cm、7cm、15cm，
∵7+7=14<15，
∴不能组成三角形，
②7cm是底边时，三角形的三边分别为7cm、15cm、15cm，
能组成三角形，
周长=7+15+15=37cm，
综上所述，它的周长是37cm.
故答案为：37cm. 在Rt△ABC中，∠C=90°，CD是斜边AB上的高，如果CD=3，BD=2．求cos∠A的值.
【解析】分析：根据题意画出图形，进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可．
本题解析：
如图所示：
∵∠ACB=90°，∴∠B+∠A=90°，
∵CD⊥AB，∴∠CDA=90°，∴∠B+∠BCD=90°，∴∠BCD=∠A，
∵CD=3，BD=2，∴BC=
∴cosA=cos∠BCD=
故答案为：