题目内容
9.已知a、b、c是△ABC的三边,且a、b、c的取值使分式$\frac{ab-ac+{c}^{2}-bc}{a-b}$的值为零,试判断这个三角形的形状,并说明理由.分析 根据分式值为零的条件,可得分子为零,根据因式分解,可得答案.
解答 解:这个三角形是等腰三角形,理由如下
由题意,得
ab-ac+c2-bc=0,且a-b≠0.
(ab-bc)-(ca-c2)=0,
b(a-c)-c(a-c)=0
(a-c)(b-c)=0,
得a=c或b=c,
这个三角形是等腰三角形.
点评 本题考查了分式值为零的条件,利用因式分解得出(a-c)(b-c)=0是解题关键.

练习册系列答案
相关题目
7.一长方形的长为8,对角线长为10,则它的面积为( )
| A. | 48 | B. | 40 | C. | 30 | D. | 12 |
14. 如图是一个三角形的算法图,每个方框里有一个数,这个数等于它所在边的两个圆圈里的数的和,则图中①②③三个圆圈里的数依次是( )
如图是一个三角形的算法图,每个方框里有一个数,这个数等于它所在边的两个圆圈里的数的和,则图中①②③三个圆圈里的数依次是( )
 如图是一个三角形的算法图,每个方框里有一个数,这个数等于它所在边的两个圆圈里的数的和,则图中①②③三个圆圈里的数依次是( )
如图是一个三角形的算法图,每个方框里有一个数,这个数等于它所在边的两个圆圈里的数的和,则图中①②③三个圆圈里的数依次是( )| A. | 19,7,14 | B. | 11,20,19 | C. | 14,7,19 | D. | 7,14,19 |
19.盒中有3个大小相同的小球,其中2个为白色,1个为红色,每次从袋中摸1个球,然后放回搅匀再摸,在摸球实验中得到下表中部分数据.
(1)请将数据表补充完整;
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
 如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为5cm.
如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为5cm.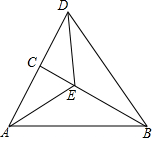 如图,已知在△ABC中,∠ACB=90°,∠BAC=60°,AE是∠BAC的平分线,延长AC至点D,使CD=AC.
如图,已知在△ABC中,∠ACB=90°,∠BAC=60°,AE是∠BAC的平分线,延长AC至点D,使CD=AC.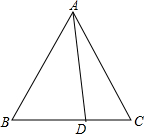 如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.
如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.