题目内容
1.一直角三角形的两直角边之比为2:3,若斜边上的高分斜边为两线段,则较小的一段与较大的一段之比是4:9.分析 画出图形,根据射影定理,得到AC2=AD×AB,BC2=BD×BA,再根据$\frac{AC}{BC}$=$\frac{2}{3}$,即可得到$\frac{4}{9}$=$\frac{AD}{BD}$.
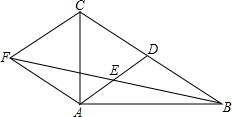
解答  解:如图所示,Rt△ABC中,CD⊥AB,
解:如图所示,Rt△ABC中,CD⊥AB,
∴AC2=AD×AB,BC2=BD×BA,
∴$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD×AB}{BD×BA}$=$\frac{AD}{BD}$,
又∵$\frac{AC}{BC}$=$\frac{2}{3}$,
∴$\frac{4}{9}$=$\frac{AD}{BD}$,
故答案为:4:9.
点评 本题主要考查了射影定理,解题时注意:每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.

练习册系列答案
相关题目
20.在实数0、$\sqrt{5}$、2、-3中,最大的数是( )
| A. | 0 | B. | $\sqrt{5}$ | C. | 2 | D. | -3 |
 如图,在△ABC中,AD是边BC上的中线,E是AD的中点,过点A作BC的平行线AF交BE的延长线于点F,连接CF.
如图,在△ABC中,AD是边BC上的中线,E是AD的中点,过点A作BC的平行线AF交BE的延长线于点F,连接CF.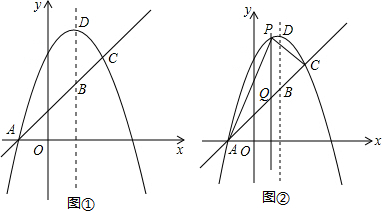
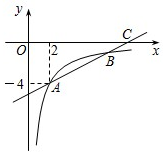 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.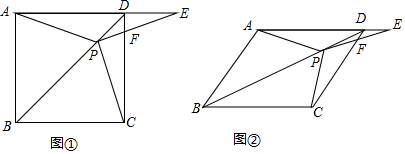
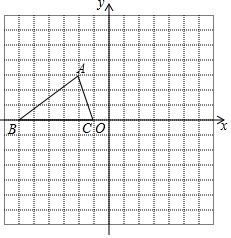 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题: