题目内容
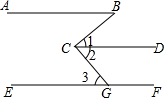如图，已知：AB∥CD∥EF，∠B=40°，∠BCG=85°，求∠3的度数．考点：平行线的性质
专题：
分析：由AB∥CD可得：∠B=∠1，进而求出∠1=40°，然后根据∠BCG=85°，可求∠2的度数为：45°，最后根据CD∥EF，可得：∠2=∠3，从而求出∠3的度数．
解答：解：∵AB∥CD，
∴∠B=∠1，
∵∠B=40°，
∴∠1=40°，
∵∠BCG=85°，
∴∠2=∠BCG-∠1=45°，
∵CD∥EF，
∴∠3=∠2=45°．
∴∠B=∠1，
∵∠B=40°，
∴∠1=40°，
∵∠BCG=85°，
∴∠2=∠BCG-∠1=45°，
∵CD∥EF，
∴∠3=∠2=45°．
点评：本题主要利用平行线的性质求解，熟练掌握性质是解题的关键．
练习册系列答案
相关题目
（1）用直尺和圆规作出△ABC的外接圆O（不写作法，保留作图痕迹）；已知等腰△ABC内接于半径为5的⊙O，如果底边BC的长为6，则底角的正切值为（ ）
| A、3 | ||||
B、
| ||||
C、3或
| ||||
D、3或
|
抛物线y=2+6x-x2的顶点坐标为（ ）
| A、（3，11） | ||||
| B、（-3，-25） | ||||
C、（
| ||||
| D、（6，2） |
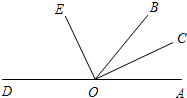如图，点O是直线AD上一点，射线OC、OE分别是∠AOB、∠BOD的平分线，∠COE=（ ）°．| A、60 | B、70 |
| C、90 | D、不能确定 |
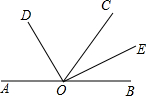如图，A、O、B三点在同一直线上，OC是任一条射线，OD、OE分别是∠AOC和∠BOC的平分线．