题目内容
已知线段AB的长为12cm,先取它的中点C,再取BC的中点D,最后取AD的中点E,那么EC等于 cm.
考点:两点间的距离
专题:
分析:根据题意分别求出AC,BC的长,进而得出DC,BC,AE的长,即可得出EC的长.
解答: 解:如图所示:∵线段AB的长为12cm,先取它的中点C,
解:如图所示:∵线段AB的长为12cm,先取它的中点C,
∴AC=BC=6cm,
∵取BC的中点D,
∴DC=BD=3cm,
∵取AD的中点E,
∴AE=DE=
AD=
(AC+CD)=
×(6+3)=4.5(cm),
∴EC=AC-AE=6-4.5=1.5(cm).
故答案为:1.5.
 解:如图所示:∵线段AB的长为12cm,先取它的中点C,
解:如图所示:∵线段AB的长为12cm,先取它的中点C,∴AC=BC=6cm,
∵取BC的中点D,
∴DC=BD=3cm,
∵取AD的中点E,
∴AE=DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴EC=AC-AE=6-4.5=1.5(cm).
故答案为:1.5.
点评:此题主要考查了两之间的距离,正确利用线段中点的性质得出是解题关键.

练习册系列答案
相关题目
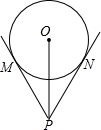 一个钢管放在V型架内,其截面如图,O为钢管界面圆的圆心,若PM=25
一个钢管放在V型架内,其截面如图,O为钢管界面圆的圆心,若PM=25| 3 |
| A、50cm | ||
B、25
| ||
| C、20cm | ||
| D、25cm |
下列三条线段的长度能组成三角形的是( )
| A、2,4,8 |
| B、4,7,11 |
| C、2,2,3 |
| D、3,6,10 |
 如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )
如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )| A、20° | B、25° |
| C、30° | D、35° |
 如图,小明在测量旗杆高度的实践活动中,发现地面上有一滩积水,他刚好能从积水中看到旗杆的顶端,测得积水与旗杆底部距离CD=6米,他与积水的距离BC=1米,他的眼睛距离地面AB=1.5米,则旗杆的高度DE=
如图,小明在测量旗杆高度的实践活动中,发现地面上有一滩积水,他刚好能从积水中看到旗杆的顶端,测得积水与旗杆底部距离CD=6米,他与积水的距离BC=1米,他的眼睛距离地面AB=1.5米,则旗杆的高度DE=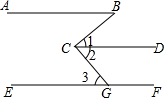 如图,已知:AB∥CD∥EF,∠B=40°,∠BCG=85°,求∠3的度数.
如图,已知:AB∥CD∥EF,∠B=40°,∠BCG=85°,求∠3的度数. 如图,指出图形中的同位角,内错角及同旁内角.
如图,指出图形中的同位角,内错角及同旁内角.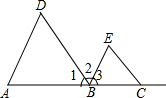 如图,
如图,