题目内容
 (1)用直尺和圆规作出△ABC的外接圆O(不写作法,保留作图痕迹);
(1)用直尺和圆规作出△ABC的外接圆O(不写作法,保留作图痕迹);(2)若BC=5
| 3 |
考点:作图—复杂作图,三角形的外接圆与外心
专题:
分析:(1)首先作出AB、BC的垂直平分线,两线的交点就是外接圆的圆心;
(2)根据圆周角定理可得∠BOC=120°,再根据等腰三角形的性质可得∠BOH=60°,BH=
BC=
,然后利用三角函数求出BO的长即可.
(2)根据圆周角定理可得∠BOC=120°,再根据等腰三角形的性质可得∠BOH=60°,BH=
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
解答: 解:(1)如图所示:
解:(1)如图所示:
(2)连接BO,CO,
∵∠A=60°,
∴∠BOC=120°,
∵EF是BC的垂直平分线,BO=CO,
∴∠BOH=60°,BH=
BC=
,
∴∠OBH=30°,
∴BO=
=5.
 解:(1)如图所示:
解:(1)如图所示:(2)连接BO,CO,
∵∠A=60°,
∴∠BOC=120°,
∵EF是BC的垂直平分线,BO=CO,
∴∠BOH=60°,BH=
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
∴∠OBH=30°,
∴BO=
| BH |
| cos30° |
点评:此题主要考查了复杂作图,以及圆周角定理和垂径定理,关键是掌握三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
下列说法正确的是( )
| A、射线PA和射线AP是同一条射线 |
| B、射线OA的长度是12cm |
| C、直线ab、cd相交于点M |
| D、两点确定一条直线 |
抛物线y=-2(x-3)2+1的顶点坐标是( )
| A、(-3,1) |
| B、(3,1) |
| C、(1,3) |
| D、(1,-3) |
 如图,AD∥BC.
如图,AD∥BC.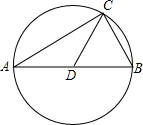 如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.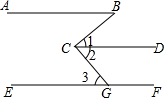 如图,已知:AB∥CD∥EF,∠B=40°,∠BCG=85°,求∠3的度数.
如图,已知:AB∥CD∥EF,∠B=40°,∠BCG=85°,求∠3的度数.