题目内容
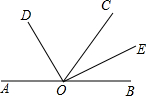 如图,A、O、B三点在同一直线上,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线.
如图,A、O、B三点在同一直线上,OC是任一条射线,OD、OE分别是∠AOC和∠BOC的平分线.(1)请你直接写出图中∠COE的余角和∠AOE的补角;
(2)当∠BOE=25°时,求∠COD的度数.
考点:余角和补角
专题:
分析:(1)容易求出∠DOC+∠COE=90°,∠AOE+∠BOE=180°,即可得出∠COE的余角是∠AOD和∠DOC,∠AOE的补角是∠COE和∠BOE;
(2)先求出∠BOC=50°,再得出∠AOC=130°,即可求出∠COD的度数.
(2)先求出∠BOC=50°,再得出∠AOC=130°,即可求出∠COD的度数.
解答:解:(1)∠COE的余角有∠AOD和∠DOC,∠AOE的补角有∠COE和∠BOE;
(2)∵OE是∠BOC的平分线,且∠BOE=25°,
∴∠BOC=2∠BOE=50°,
∴∠AOC=180°-∠BOC=130°.
又∵OD是∠AOC的平分线,
∴∠COD=
∠AOC=
×130°=65°.
(2)∵OE是∠BOC的平分线,且∠BOE=25°,
∴∠BOC=2∠BOE=50°,
∴∠AOC=180°-∠BOC=130°.
又∵OD是∠AOC的平分线,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了余角和补角的定义;弄清各个角之间的关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,DE∥BC,则下列比例式错误的是( )
如图,DE∥BC,则下列比例式错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )
如图,△ABC是圆O的内接三角形,若∠OBC=70°,则∠A的度数是( )| A、20° | B、25° |
| C、30° | D、35° |
已知
=
=
=k,则k的取值为( )
| a |
| b+c |
| b |
| c+a |
| c |
| b+a |
A、
| ||
| B、-1 | ||
C、
| ||
D、-
|
估算实数
的大小时,若使误差小于1,则结果应为( )
| 3 | 90 |
| A、3或4 | B、4或5 |
| C、5或6 | D、9或10 |
点A(x1,y1),B(x2,y2),C(x3,y3)分别是y=-
图象上三点,且x1>x2>0>x3,则下列结论正确的是( )
| 1 |
| x |
| A、y1>y2>y3 |
| B、y1>y3>y2 |
| C、y3>y1>y2 |
| D、y1>y2>y3 |
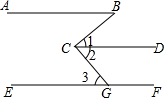 如图,已知:AB∥CD∥EF,∠B=40°,∠BCG=85°,求∠3的度数.
如图,已知:AB∥CD∥EF,∠B=40°,∠BCG=85°,求∠3的度数. 如图,点A、B在数轴上分别表示有理数a、b,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:
如图,点A、B在数轴上分别表示有理数a、b,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题: 如图所示,已知∠1=∠2,DE∥BC,你能判断出图形中还有哪些角是相等的吗?(写出两对相等角即可)
如图所示,已知∠1=∠2,DE∥BC,你能判断出图形中还有哪些角是相等的吗?(写出两对相等角即可)