题目内容
9.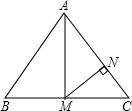 如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )
如图在△ABC中,AB=AC=10,BC=12,点M为BC的中点,MN⊥AC于点N,则MN等于( )| A. | $\frac{12}{5}$ | B. | $\frac{18}{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{32}{5}$ |
分析 先根据等腰三角形的性质求出BM,CM,A再用勾股定理就算即可.
解答 解:∵AB=AC=10,点M为BC的中点,
∴AM⊥BC,BM=CM=$\frac{1}{2}$BC=6
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{100-36}$=8,
∵MN⊥AC,
∴S△AMC=$\frac{1}{2}$AC×MN.
∵S△AMC=$\frac{1}{2}$AM×MC.
∴AC×MN=AM×MC,
∴10MN=8×6
∴MN=$\frac{24}{5}$,
故选C,
点评 此题是等腰三角形的性质,三角形的面积的计算,解本题的关键是同一个三角形的面积用两种不同的算法,求出MN,

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.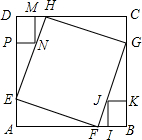 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )| A. | 10 | B. | 3$\sqrt{10}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{10}$或4$\sqrt{5}$ |
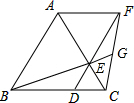 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论: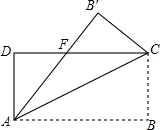 如图,在矩形ABCD中,AB=8,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为( )
如图,在矩形ABCD中,AB=8,BC=4,将矩形AC折叠,点B落在点B′处,重叠部分△AFC的面积为( )
 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.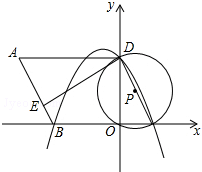 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.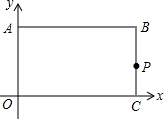 如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6中上的一点.若△APD是等腰Rt△,则点D的坐标为(4,2)或($\frac{20}{3}$,$\frac{22}{3}$)或($\frac{28}{3}$,$\frac{38}{3}$).
如图,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6中上的一点.若△APD是等腰Rt△,则点D的坐标为(4,2)或($\frac{20}{3}$,$\frac{22}{3}$)或($\frac{28}{3}$,$\frac{38}{3}$).