题目内容
19.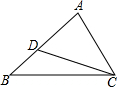 如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.
如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.
分析 由∠A=∠A,∠ACD=∠B,得到△ABC∽△ACD,根据相似三角形的性质得到对应边成比例,代入数据即可得到结果.
解答 解:∵∠A=∠A,∠ACD=∠B,
∴△ABC∽△ACD,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
即$\frac{8}{10}=\frac{AD}{8}$,
解得:AD=6.4.
故答案为:6.4.
点评 本题考查了相似三角形的性质和判定的应用,注意:①相似三角形的对应边的比相等,②有两角对应相等的两三角形相似.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.有下列长度的三条线段,能组成三角形的是( )
| A. | 2cm,3cm,4cm | B. | 1cm,4cm,2cm | C. | 1cm,2cm,3cm | D. | 6cm,2cm,3cm |
4.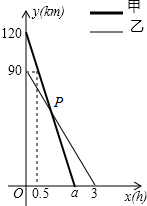 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )| A. | A、C两村间的距离为120km | |
| B. | 点P的坐标为(1,60) | |
| C. | 点P的意义表示经过1小时甲与乙相遇且距C村60km | |
| D. | 乙在行驶过程中,仅有一次机会距甲10km |
8.如图,利用尺规作的角平分线OC,在用尺规作角平分线时,用到的三角形全等的判定方法是( )
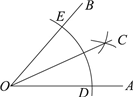 | 作法:①以O为圆心,任意长为半径作弧,交OA,OB于点D,E. ②分别以D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内交于点C. ③作射线OC.则OC就是∠AOB的平分线. |
| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
9.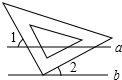 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )| A. | 45° | B. | 36° | C. | 54° | D. | 126° |
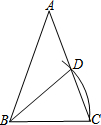 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.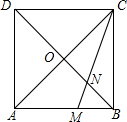 如图,正方形ABCD的边长为3,对角线AC与BD相交于点O,CM交BD于点N,若BM=1,则线段ON的长为$\frac{3\sqrt{2}}{4}$.
如图,正方形ABCD的边长为3,对角线AC与BD相交于点O,CM交BD于点N,若BM=1,则线段ON的长为$\frac{3\sqrt{2}}{4}$.