题目内容
20.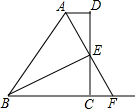 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.(1)BE平分∠ABC吗?若平分,请说明理由.
(2)AE与BE有何位置关系?请说明理由.
(3)AD、BC与AB之间有何数量关系?请说明理由.
分析 (1)根据平行线的性质得到∠1=∠5,根据角平分线的定义得到∠1=∠2,等量代换得到∠2=∠5,得到AB=BF,根据等腰三角形的性质得到DE=EF,根据全等三角形的性质得到AE=EF,于是得到结论;
(2)根据等腰三角形的性质即可得到结论;
(3)根据全等三角形的性质即可得到结论.
解答 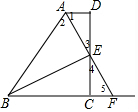 解:(1)BE平分∠ABC,
解:(1)BE平分∠ABC,
理由:∵AD∥BC,
∴∠1=∠5,
∵AE平分∠BAD,
∴∠1=∠2,
∴∠2=∠5,
∴AB=BF,
∵E是DC的中点,
∴DE=EF,
在△ADE与△EFC中,$\left\{\begin{array}{l}{∠1=∠5}\\{∠3=∠4}\\{DE=EF}\end{array}\right.$,
∴△ADE≌△FCE,
∴AE=EF,
∴BE平分∠ABC;
(2)AE⊥BE,
理由:∵AB=BF,AE=EF,
∴AE⊥BE;
(3)AB=BC+AD,
理由:∵△ADE≌△FCE,
∴AD=CF,
∵AB=BF=BC+CF,
∴AB=BC+AD.
点评 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,角平分线的性质.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.
如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E. 如图,AB=AD,CB=CD,求证:∠B=∠D.
如图,AB=AD,CB=CD,求证:∠B=∠D.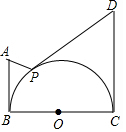 (1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.
(1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.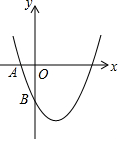 如图,函数y=x2-2x-3与坐标轴交于A、B两点,问抛物线上是否存在点C使四边形ABCO为平行四边形,若存在,求出点C的坐标;若不存在,说明理由.
如图,函数y=x2-2x-3与坐标轴交于A、B两点,问抛物线上是否存在点C使四边形ABCO为平行四边形,若存在,求出点C的坐标;若不存在,说明理由. 如图,已知等腰Rt△ABC中,∠A=90°,BD平分∠ABC,过C作BD的垂线CE.求证:BD=2CE.
如图,已知等腰Rt△ABC中,∠A=90°,BD平分∠ABC,过C作BD的垂线CE.求证:BD=2CE. 一段抛物线:y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$(0≤x≤3)记为C1,它与x轴交于点O,A1:将C1绕点A1旋转180°得到C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13,若P(37,m)在第13段抛物线C13上,则m=2.
一段抛物线:y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$(0≤x≤3)记为C1,它与x轴交于点O,A1:将C1绕点A1旋转180°得到C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13,若P(37,m)在第13段抛物线C13上,则m=2.