题目内容
15.阅读题:通过学习,爱好思考的小明发现,一元二次方程的根完全由它的系数确定,即一元二次方程ax2+bx+c=0(a≠0),当b2-4ac≥0时有两个实数根:x1=$\frac{{-b+\sqrt{{b^2}-4ac}}}{2a}$,x2=$\frac{{-b-\sqrt{{b^2}-4ac}}}{2a}$,于是:x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$这就是著名的韦达定理.请你运用上述结论解决下列问题:
关于x的一元二次方程x2+kx+k+1=0的两实数根分别为x1、x2,且x12+x22=1,求:k的值是多少?
分析 根据韦达定理可得x1+x2=-k,x1x2=1,将其代入到x12+x22=1,即(x1+x2)2-2x1x2=1,解关于k的方程可得k的值,再代回方程检验可得.
解答 解:∵方程x2+kx+k+1=0的两实数根分别为x1、x2,
∴x1+x2=-k,x1x2=k+1,
∵x12+x22=1,即(x1+x2)2-2x1x2=1,
∴k2-2(k+1)=1,
解得:k=-1或k=3,
当k=-1时,方程为x2-x=0,解得:x=0或x=1;
当k=3时,方程为x2+3x+4=0,方程无解,
∴k=-1.
点评 本题主要考查一元二次方程根与系数的关系,熟练掌握韦达定理是解题的关键.

练习册系列答案
相关题目
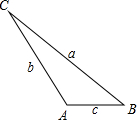 如图,已知△ABC中,∠B=2∠C,a,b,c为三边长.
如图,已知△ABC中,∠B=2∠C,a,b,c为三边长.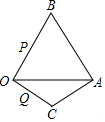 已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:
已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题: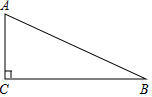 已知△ABC中,∠C=90°,AC=8cm,AB=17cm.
已知△ABC中,∠C=90°,AC=8cm,AB=17cm.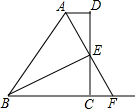 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.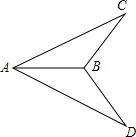 如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.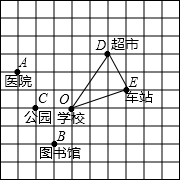 如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题:
如图,10×10的正方形网格(每个小正方形的边长为1)表示某市部分简图,学校,医院、图书馆、公园、超市、车站的位置分别用点O、A、B、C、D、E表示,请你完成下列问题: