题目内容
10. 如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.
如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.求证:△DME∽△BCA.
分析 先证明∠DEM=∠A,再由∠C=∠DME=90°,根据有两组角对应相等的两个三角形相似即可证明△DME∽△BCA.
解答 证明:∵∠C=90°,DM⊥AB于点M,DN⊥BC于点N,
∴∠C=∠ENB=∠DME=90°,
∴AC∥DN,
∴∠BEN=∠A,
∵∠BEN=∠DEM,
∴∠DEM=∠A.
在△DME与△BCA中,
$\left\{\begin{array}{l}{∠DEM=∠A}\\{∠DME=∠C}\end{array}\right.$,
∴△DME∽△BCA.
点评 本题考查了相似三角形的判定,方法有(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 如图,在一次定向越野活动中,“超越”小组准备从目前所在的A 处前往相距2km的B处,则相对于A处来说,B处的位置是( )
如图,在一次定向越野活动中,“超越”小组准备从目前所在的A 处前往相距2km的B处,则相对于A处来说,B处的位置是( )
 如图,在一次定向越野活动中,“超越”小组准备从目前所在的A 处前往相距2km的B处,则相对于A处来说,B处的位置是( )
如图,在一次定向越野活动中,“超越”小组准备从目前所在的A 处前往相距2km的B处,则相对于A处来说,B处的位置是( )| A. | 南偏西50°,2km | B. | 南偏东50°,2km | C. | 北偏西40°,2km | D. | 北偏东40°,2km |
1.化简|3-π|的结果为( )
| A. | 0 | B. | 3-π | C. | π-3 | D. | 3+π |
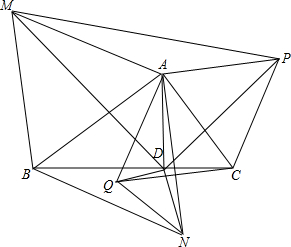 AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.
AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.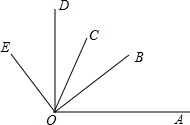 如图,OB是∠AOC的平分线,OD是∠COE的平分线.
如图,OB是∠AOC的平分线,OD是∠COE的平分线.
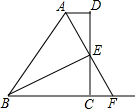 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.