题目内容
9.已知关于x的方程ax2+bx+c=0,其中2a+3b+6c=0.(1)当a=0时,求方程的根;
(2)当a>0时,求证:方程有一根在0和1之间.
分析 (1)将a=0代入2a+3b+6c=0可得c=-$\frac{b}{2}$,将a=0、c=-$\frac{b}{2}$代入方程后求解可得;
(2)令f(x)=ax2+bx+c,根据2a+3b+6c=0可得f($\frac{1}{2}$)=$\frac{a}{4}$+$\frac{b}{2}$+c=$\frac{a}{3}$+$\frac{b}{2}$+c-$\frac{a}{12}$=-$\frac{a}{12}$<0,由f(0)=c可分c>0和c≤0两种情况讨论:①c>0时,由f($\frac{1}{2}$)<0、f(0)>0可知方程有一根在0和1之间;②c≤0时,由f($\frac{2}{3}$)=$\frac{4a+6b+12c-3c}{9}$=-$\frac{c}{3}$≥0、f(0)=c≤0可知方程有一根在0和1之间,得证.
解答 解:(1)当a=0,由2a+3b+6c=0可得c=-$\frac{b}{2}$,
方程为bx-$\frac{b}{2}$=0,
解得:x=$\frac{1}{2}$;
(2)设f(x)=ax2+bx+c,
则f($\frac{1}{2}$)=$\frac{a}{4}$+$\frac{b}{2}$+c=$\frac{a}{3}$+$\frac{b}{2}$+c-$\frac{a}{12}$,
∵2a+3b+6c=0,且a>0
∴$\frac{a}{3}$+$\frac{b}{2}$+c=0,
∴f($\frac{1}{2}$)=-$\frac{a}{12}$<0,
∵f(0)=c,
①当c>0时,由f($\frac{1}{2}$)<0、f(0)=c>0可知方程有一根在0和1之间;
②当c≤0时,
∵2a+3b+6c=0,
∴4a+6b+12c=0,
∴f($\frac{2}{3}$)=$\frac{4}{9}a$+$\frac{2}{3}$b+c=$\frac{4a+6b+12c-3c}{9}$=-$\frac{c}{3}$≥0,
∴由f(0)=c≤0,f($\frac{2}{3}$)≥0可知方程有一根在0和1之间;
综上,方程有一根在0和1之间.
点评 本题主要考查二次函数的性质、一元二次方程的解,将方程的解得问题转化为二次函数问题求解是解题的关键.

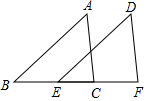 如图,AB=DE,AB∥DE,BC=EF.则下列结论中正确的是( )
如图,AB=DE,AB∥DE,BC=EF.则下列结论中正确的是( )①AC=DF ②∠A=∠D ③AC∥DF ④∠A+∠B=∠D+∠DEF.
| A. | ①② | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
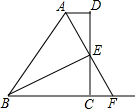 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.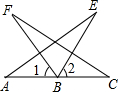 如图,B是AC中点,∠F=∠E,∠1=∠2.证明:AE=CF.
如图,B是AC中点,∠F=∠E,∠1=∠2.证明:AE=CF.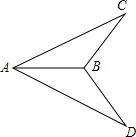 如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.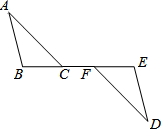 如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.
如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.