题目内容
8. (1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.
(1)已知关于x的一元二次方程(a+c)x2+bx+(a-c)=0,其中a,b,c分别为△ABC的边长.若(a,b),c分别为⊙M的圆心坐标和半径,则称⊙M为△ABC的“伴侣圆”.①当△ABC为等边三角形,求方程的根;
②当⊙M与坐标轴有三个交点时,△ABC是C 三角形;
A.等腰 B.直角 C.等腰或直角 D.等边
(2)若一元二次方程(a+c)x2+bx+(a-c)=0的根为-1和$\frac{1}{2}$,且a,b,c为连续的整数.
①求a,b,c的值;
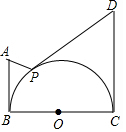
②如图,BC是半圆直径,AB⊥BC,CD⊥BC,边AB,BC,CD的长分别为a,b,c的值,P为半圆上一动点,求多边形ABCDP面积的最大值是2+$\sqrt{2}$.
分析 (1)利用△ABC是等边三角形,则a=b=c,进而代入方程求出即可.
(2)利用圆与坐标轴的位置关系即可求得,
(3)①根据三角形的面积公式和射影定理即可得到函数关系式,根据关系式即可求得.
②因为五边形ABCDP的面积=四边形ABCD的面积-△APD的面积,所以只要求出△ADP面积的最小值,
作EF∥AD,且与⊙O相切于点O,连接OP延长OP交AD于H,易知此时点P到AD的距离最小,此时△ADP的面积最小,延长即可解决问题.
解答 (1)当△ABC是等边三角形,a=b=c,
(a+c)x2+bx+(a-c)=0,
可整理为:2ax2+ax=0,
2x2+x=0,
解得:x1=0,x2=-$\frac{1}{2}$.
(2)若(a,b),c分别为⊙M的圆心坐标和半径,当圆与y轴相切时,a2+b2=c2;当圆与x轴相切时,b=c;
故△ABC是直角或等腰三角形,
故选C.
(3)①∵方程的根为-1和$\frac{1}{2}$,
∴-1+$\frac{1}{2}$=-$\frac{b}{a+c}$,-1×$\frac{1}{2}$=$\frac{a-c}{a+c}$,
∴2b=a+c,c=3a,
∴b=2a,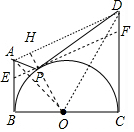
∵a,b,c为连续的整数,
∴a=1,b=2,c=3;
②∵五边形ABCDP的面积=四边形ABCD的面积-△APD的面积,
∴只要求出△ADP面积的最小值,
作EF∥AD,且与⊙O相切于点O,连接OP延长OP交AD于H,
易知此时点P到AD的距离最小,此时△ADP的面积最小,
易知AD=2$\sqrt{2}$,
∵四边形ABCD的面积=$\frac{1}{2}$(1+3)×2=4=$\frac{1}{2}$×1×1+$\frac{1}{2}$•AD•OH+$\frac{1}{2}$•1•3,
∴OH=$\sqrt{2}$,
∴PH=$\sqrt{2}$-1,
∴△PAD的面积最小值为2-$\sqrt{2}$,
∴ABCDP面积的最大值是4-(2-$\sqrt{2}$)=2+$\sqrt{2}$.
故答案为2+$\sqrt{2}$.
点评 此题是圆的综合题,主要考查了一元二次方程的应用以及根的判别式和勾股定理等知识,正确由已知获取函数关系是解题关键.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案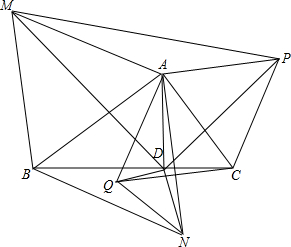 AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.
AD是Rt△ABC的垂线,以AB为边长,分别向内,外做正三角形ABN、ABM,以AC为边长,分别向内、外作正三角形ACQ、ACP,连接MD、ND、PD、QD、MP、QN,求证:△MPD相似于△NQD.
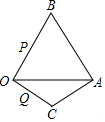 已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题:
已知:等边△OAB的边长为3,另一等腰△OCA与△OAB有公共边OA,且OC=AC,∠C=120°.现有两动点P、Q分别从B、O两点同时出发,点P以每秒3个单位的速度沿BO向点O运动,点Q以每秒1个单位的速度沿OC向点C运动,当其中一个点到达终点时,另一个点也随即停止运动.请回答下列问题: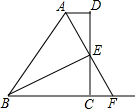 如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.
如图,AD∥BC,DC⊥AD,AE平分∠BAD,且E是DC的中点.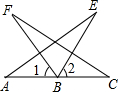 如图,B是AC中点,∠F=∠E,∠1=∠2.证明:AE=CF.
如图,B是AC中点,∠F=∠E,∠1=∠2.证明:AE=CF.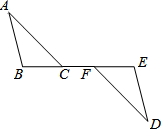 如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.
如图,C、F在BE上,∠A=∠D,AC∥DF,BF=EC.你知道AB与DE有什么关系?请说明理由.